1 本章概要
密码的本质就是将较长得密码——消息,变成较短的密码——秘钥。
2 什么是秘钥
2.1 秘钥就是一个巨大的数字
在使用对称密码、公钥密码、消息认证码、数字签名等密码技术,都需要一个称为秘钥(key)的巨大数字。然后,数字本身的带下并不重要,重要的是秘钥空间的大小,也就是可能出现的秘钥的总数量,因为秘钥空间越大,进行暴力破解就越困难。秘钥空间的大小是由秘钥长度决定的。
1.DES 的秘钥
对称密码 DES 的秘钥的实质长度为 56 比特。
例如,一个 DES 秘钥用二进制可以表示为:
01010001 10100101 10100011 10101010 01101101 10100001 11100011 00100100
用十六进制则可以表示为:
51 EC 4B 12 3D 4A A1
而用十进制则可以表示为:
12309120398102938102983
为了显得专业,将统一使用十六进制。
2.三重 DES 的秘钥
在对称密码三重 DES 中,包括使用两个 DES 秘钥的 DES-EDE2 和使用三个 DES 秘钥的 DES-EDE3 两种方式。
DES-EDE2 的秘钥实际长度为 112 比特。
DES-EDE3 的秘钥实际长度为 168 比特。
3.AES 的秘钥
对称密码 AES 的秘钥长度可以从 128、192和 256 比特中进行选择。
实际长度会更长,因为会加一些用于识别通信错误的校验比特。
2.2 秘钥和明文是等价的
对于窃听密文的 Eve 来说,得到秘钥和得到明文是等价的。即,秘钥和明文是等价的。假设明文具有 100 万元的价值,那么用来加密这段明文的秘钥也就具有 100 万元的价值。
2.3 密码算法与秘钥
信息的机密性不应该依赖于密码算法本身,而是应该依赖于妥善保管的秘钥。这是密码世界的赏识之一。
3 各种不同的秘钥
3.1 对称密码的秘钥与公钥密码的秘钥
在对称密码中,加密和解密使用同一个秘钥。由于发送者和接收者之间需要共享秘钥,因此对称密码又称为共享秘钥密码。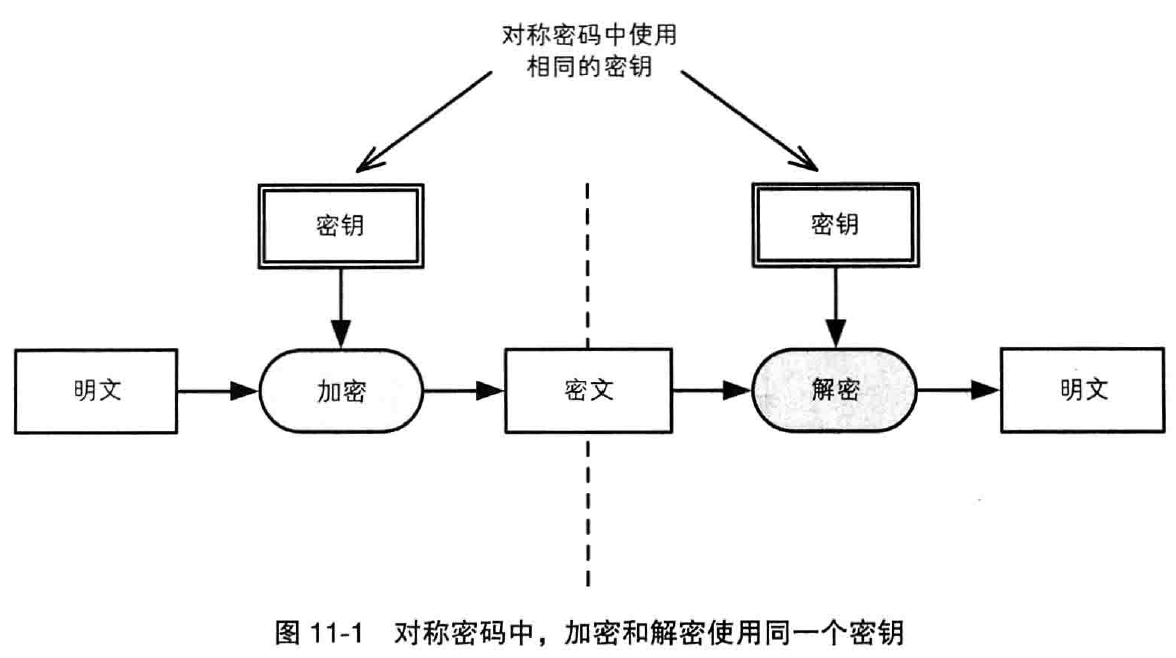
在公钥密码中,加密和解密使用的是不同的秘钥。用于加密的秘钥称为公钥;用于解密的秘钥称为私钥。公钥可以被公开,私钥只能被解密者拥有。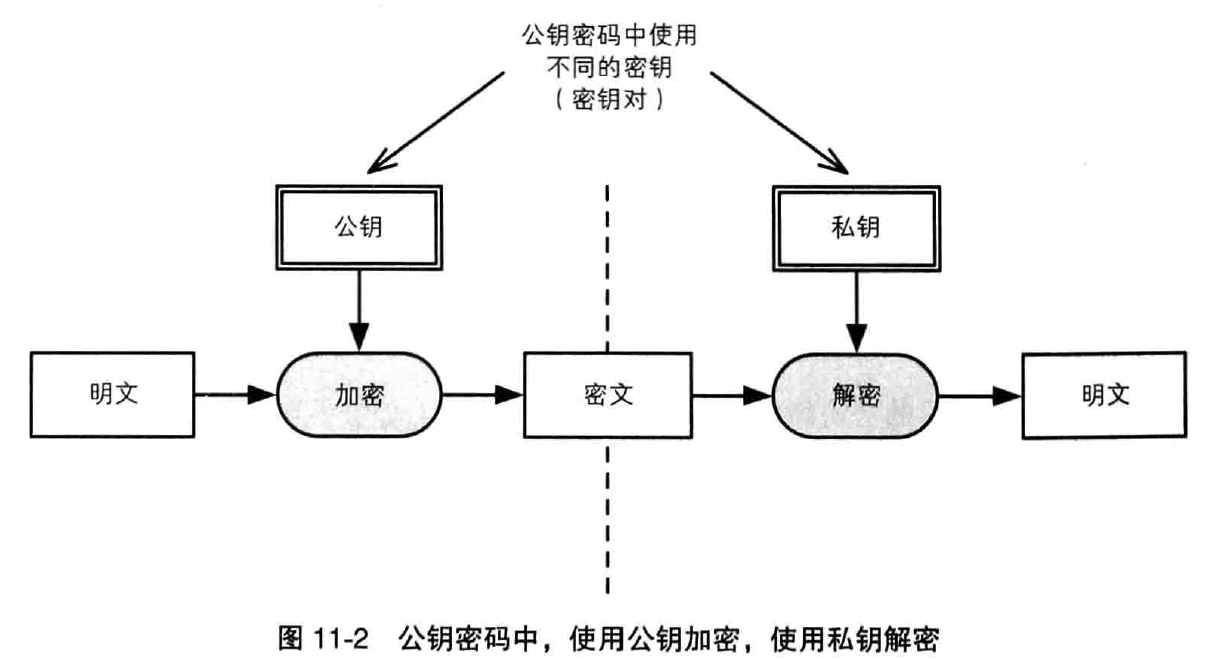
3.2 消息认证码的秘钥与数字签名的秘钥
在消息认证码中,发送者和接收者使用共享的秘钥来进行认证。消息认证码只能由持有合法秘钥的人计算出来。将消息认证码附加在通信报文后面,就可以识别通信内容是否被篡改或伪装。由于“持有合法的秘钥”就是发送者和接收者合法身份的证明,因此消息认证码的秘钥必须对发送者和接收者以外的人保密,否则就会产生篡改和伪装的风险。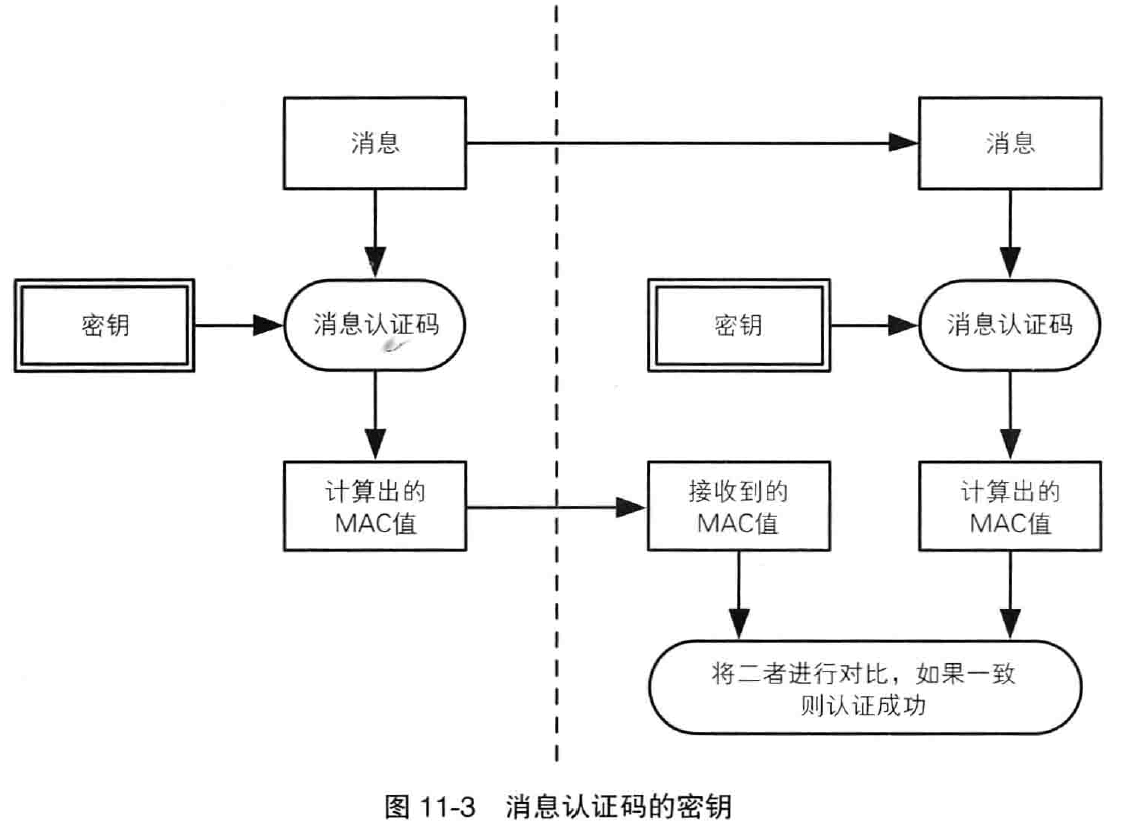
在数字签名中,签名的生成和验证使用不同的秘钥。只有持有私钥的本人才能够生成签名,但由于验证签名使用的是公钥,因此任何人都能够验证签名。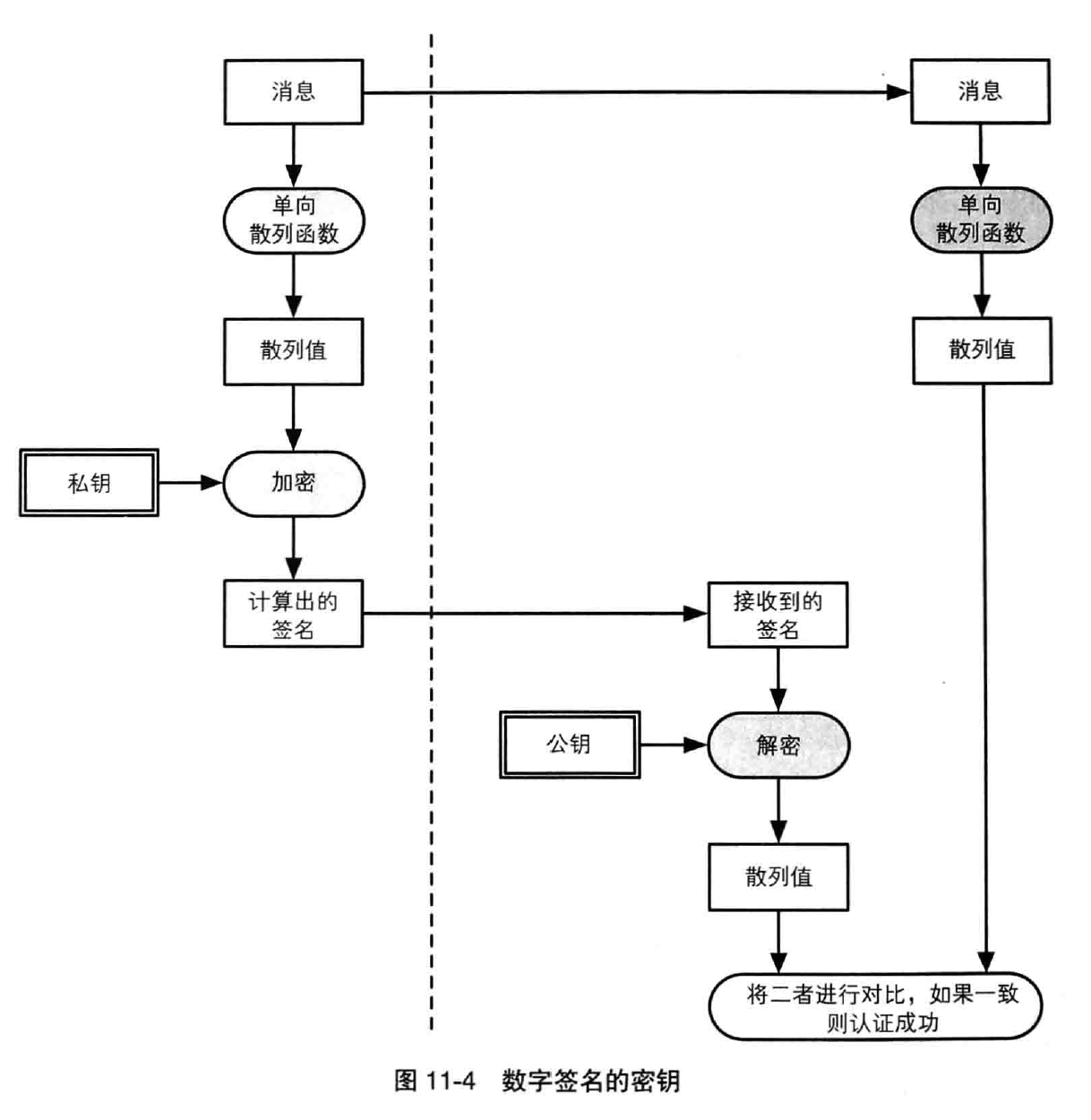
3.3 用于确保机密性的秘钥与用于认证的秘钥
对称密码和公钥密码的秘钥都是用于确保机密性的秘钥。如果不知道用于解密的合法秘钥,就无法得知明文的内容。
相对地,消息认证码和数字签名所使用的秘钥,则是用于认证的秘钥。如果不知道合法的秘钥,就无法篡改数据,也无法伪装本人的身份。
3.4 会话秘钥与主秘钥
刚刚我们关注的是秘钥的用途,下面我们来关注一下秘钥被使用的次数。
当我们访问以 https:// 开头的网页时,Web 服务器和浏览器之间会进行基于 SSL/TLS 的加密通信。在这样通信中所使用的秘钥仅限于本次通信的一次性秘钥,下次通信时就不能使用了。像这样每次通信只能使用一次的秘钥称为会话秘钥(session key)。
虽然每次通信都会更会秘钥,但如果用来生成秘钥的伪随机数生成器品质不好,窃听者就有可能预测出下次生成的会话秘钥,这样就会产生内容被破译的风险。
相对于每次通信都更换的会话秘钥,一直被重复使用的秘钥称为主秘钥(master key)。
3.5 用于加密内容的秘钥与用于加密秘钥的秘钥
一般来说,加密的对象使用户直接使用的信息,这样的情况下所使用的秘钥称为 CEK(Contents Encrypting Key,内容加密秘钥);相对地,用于加密秘钥的秘钥则称为 KEK(Key Encrypting Key,秘钥加密秘钥)。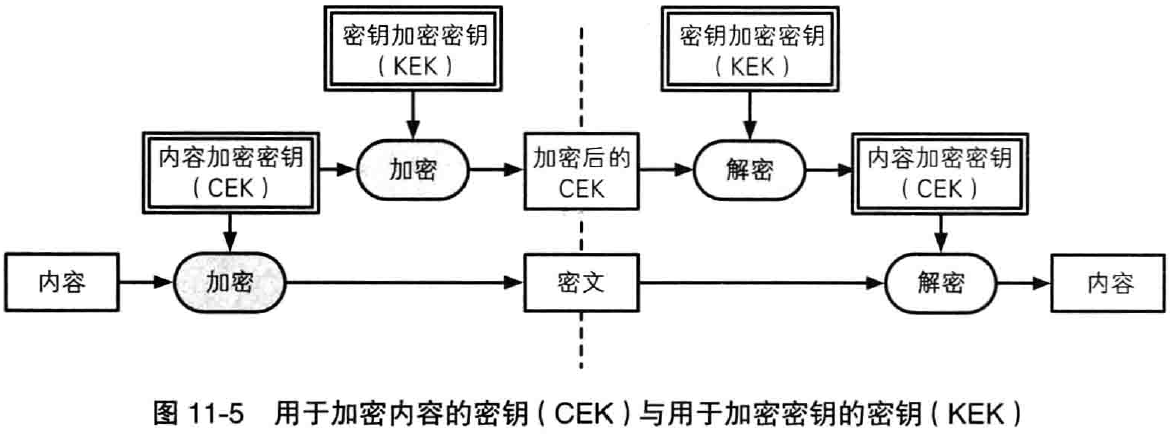
在很多情况下,之前提到的会话秘钥都是被作为 CEK 使用的,而主秘钥则是被作为 KEK 使用的。
4 秘钥的管理
4.1 生成秘钥
1.用随机数生成秘钥
2.用口令生成秘钥
即人类可以记住的口令(password或passphrase)生成秘钥,但是由字典攻击。
4.2 配送秘钥
在第五章介绍,可以采用事先共享秘钥、使用秘钥分配中心、使用公钥密码等方法。一会将介绍Diffie-Hellman秘钥交换。
4.3 更新秘钥
有一种提高通信机密性的技术被称为秘钥更新(key updating),这种方法就是在使用共享秘钥进行通信的过程中,定期(例如每发送 1000 个字)改变秘钥。
在更新秘钥时,发送者和接收者使用单向散列函数计算当前秘钥的散列值,并将这个散列值用作新的秘钥。简单说,就是用当前秘钥的散列值作为下一个秘钥。
这种防止破译过去的通信内容的机制,称为后向安全(backward security)。
4.4 保存秘钥
由于会话秘钥在通信过程中仅限使用一次,因此我们不需要保存这种秘钥。然而,当秘钥需要重复使用时,就必须要考虑保存秘钥的问题了。
1.人类无法记住秘钥
首先我们必须要理解一个重要的事实,那就是人类是无法记住具有使用长度的秘钥的。
2.对秘钥进行加密的意义
例如,计算机上有 100 万个文件,分别使用不同的秘钥进行加密生成 100 万个密文,结果我们手上就产生了 100 万个秘钥。于是,我们用一个秘钥将这 100 万个秘钥进行加密,那么我们只要保管这一个秘钥就行了。
4.5 作废秘钥
如果秘钥是计算机上的一个文件,那么仅仅删除这个文件是不足以删除秘钥的,此外,很多情况下文件的内容还会残留在计算机的内存中。简而言之,要完全删除秘钥,不但要用到密码软件,还需要在设计计算机系统时对信息安全进行充分的考虑。当然,还要防止秘钥丢失。
5 Diffie-Hellman秘钥交换
5.1 什么是 Diffie-Hellman 秘钥交换
使用这种算法,通信双方仅通过交换一些可以公开的信息就能够生成共享的秘密数字,而这一秘密数字就可以被用作对称密码的秘钥。 IPsec 中就使用了经过改良的 Diffie-Hellman 秘钥交换。
虽然名字叫做“秘钥交换”,但实际上双方并没有真正交换秘钥,而是通过计算机生成出了一个相同的共享秘钥。因此,这种方法也称为 Diffie-Hellman 秘钥协商(Diffie-Hellman key agreement)。
5.2 Diffie-Hellman 秘钥交换的步骤
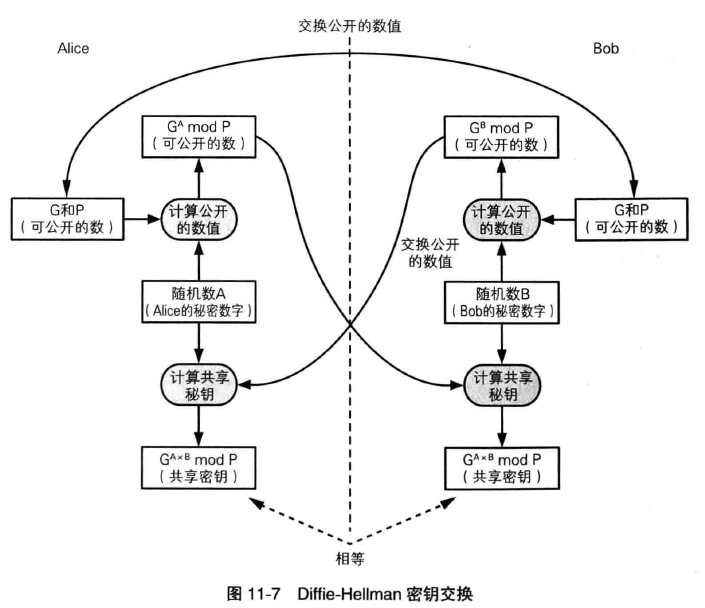
1.Alice 向 Bob 发送两个质数 P 和 G
P 必须是一个非常大的质数,而 G 则是一个和 P 相关的数,称为生成元。 G 可以是一个较小的数字。 P 和 G 不需要保密。
2.Alice 生成一个随机数 A
A 是一个 1 ~ P-2 之间的整数。这个数是一个只有 Alice 知道的秘密数字,没有必要告诉 Bob ,也不能让 Eve 知道。
3.Bob 生成一个随机数 B
B 是一个 1 ~ P-2 之间的整数。这个数是一个只有 Bob 知道的秘密数字,没有必要告诉 Alice ,也不能让 Eve 知道。
4.Alice 将 G^A mod P 这个数发送给 Bob
这个数让 Eve 知道也没关系
5.Bob 将 G^B mod P 这个数发送给 Alice
这个数让 Eve 知道也没关系
6.Alice 用 Bob 发过来的数计算 A 次方并求 mod P
这个数就是共享秘钥。 (G^B mod P)^A mod P
7.Bob 用 Alice 发过来的数计算 B 次方并求 mod P
这个数就是共享秘钥。 (G^A mod P)^B mod P
8.这样 Alice 和 Bob 得到的值就是相同的
5.3 Eve 能计算出秘钥吗
这是一个离散数学的问题,根据 G^A mod P 的值,以及 G、P 求出 A。非常的困难。
6 基于口令的密码(PBE)
6.1 什么是基于口令的密码
用口令来生成秘钥(KEK),但只用口令容易遭到字典攻击,那么就用口令和盐共同生成秘钥(KEK),盐可以和加密后的秘钥(CEK)一起保存在磁盘上,而秘钥可以直接丢弃,口令就记在脑子里吧。
6.2 PBE 加密
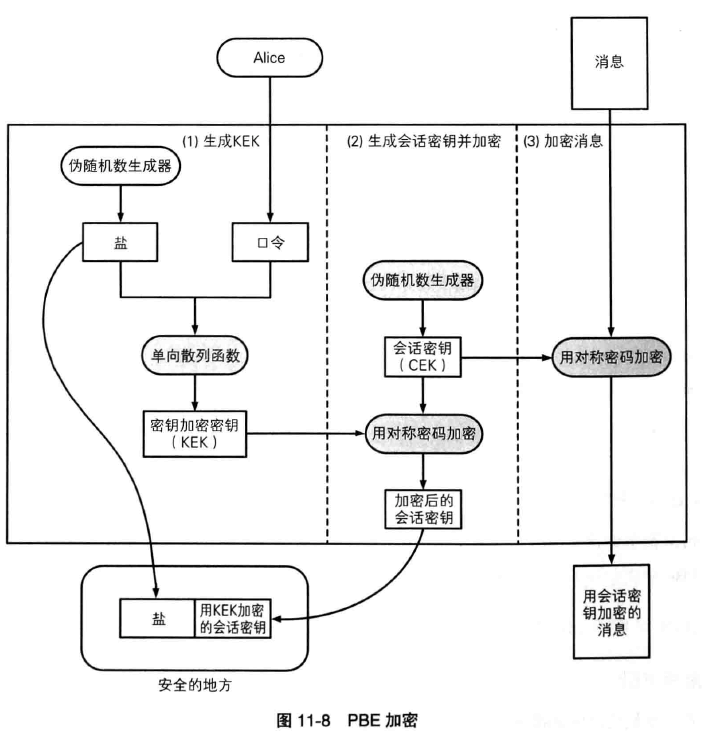
6.3 PBE 解密
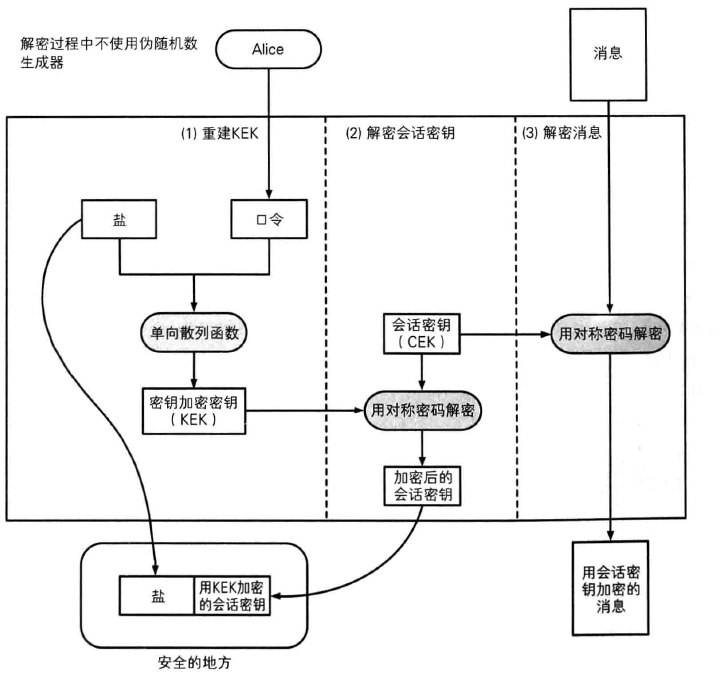
7 本章小结
对秘钥本身做了简单介绍。
8 小测验
- 由于秘钥只是随机的比特序列,因此被别人知道了也没关系。
- 私钥是可以公开的。
- 在 Diffie-Hellman 秘钥交换中,双方可以通过交换一些可以公开的信息生成出共享秘钥。