1 骡子的锁匠铺

很久很久之前，骡子开了一家锁匠铺，他说：“我做的锁头很坚固，小偷绝对打不开。”因此动物村里所有的动物都为自己的房子装上了骡子做的锁。
骡子做的锁确实很坚固，但是每把锁头上用的钥匙居然都是同一个形状的。因此小偷只要得到了一栋房子的钥匙，就可以打开所有房子的锁了。
教训：坚固的锁头固然重要，但不可预测的钥匙更加重要。

2 本章概要

• 使用随机数的密码技术
• 随机数的性质
• 伪随机数生成器
• 具体的伪随机数生成器
• 对伪随机数生成器的攻击

3 使用随机数的密码技术

3.1 随机数是干什么的

1. 生成秘钥：用于对称密码和消息认证码。
2. 生成密钥对：用于公钥密码和数字签名。
3. 生成初始化向量（IV）：用于分组密码的 CBC、CFC 和 OFB 模式。
4. 生成 nonce：用于防御重放攻击以及分组密码的 CTR 模式等。
5. 生成盐：用于基于口令的密码（PBE）等。

在这里，请大家记住为了不让攻击者看穿而使用随机数这一观点，因为“无法看穿”，及不可预测性，正是本章的主题。

4 随机数的性质

4.1 对随机数的性质分类

1. 随机性：不存在统计学偏差，是完全杂乱的数列。
2. 不可预测性：不能从过去的数列推测出下一个出现的数。
3. 不可重现性：除非将数列本身保存下来，否则不能重现相同的数列。

为了方便起见，将上述三个性质按顺序分别命名为“弱伪随机数”、“强伪随机数”和“真随机数”。
||随机性|不可预测性|不可重现性||
|:-:|:-:|:-:|:-:|:-:|
|弱伪随机数|✔️|✘|✘|只具备随机性|
|强伪随机数|✔️|✔️|✘|具备不可预测性|
|真随机数|✔️|✔️|✔️|具备不可重现性|

4.2 随机性

杂乱无章并不代表不会被看穿，因此本书中将只具备随机性的伪随机数称为“弱伪随机数”。

4.3 不可预测性

不可预测性（unpredictability），是一种“不可能事先说中”的性质，及不可预测性。即，攻击者在知道过去生成的为随机数列的前提下，依然无法预测出下一个生成出来的伪随机数的性质。

4.4 不可重现性

即，无法重现和某一随机数列完全相同的数列的性质。如果除了将随机数列本身保存下来意外，没有其它方法能够重现该数列，则我们就说该随机数列具备不可重现性。
要生成具备不可重现性的随机数列，需要从不可重现的物理现象中获取信息，比如周围的温度和声音的变化、用户移动的鼠标的位置信息、键盘输入的时间间隔、放射线测量仪的输出值等，根据从这些硬件中获取的信息而生成的数列，一般可以认为是具备不可重现性的随机数列。

5 伪随机数生成器

仅仅靠软件无法生成真随机数，因此要加上一个“伪”。

5.1 伪随机数生成器的结构

伪随机数生成器具有“内部状态”，并根据外部输入的“种子”来生成伪随机数列。

1.伪随机数生成器的内部状态

伪随机数生成器的内部状态，是指伪随机数生成器所管理的内存中的数值。伪随机数生成器会根据内存中的数值进行计算，并将计算的结果作为伪随机数输出。随后，为了响应下一个伪随机数请求。伪随机数生成器会改变自己的内部状态。

2.伪随机数生成器的种子

伪随机数的种子是用来对伪随机数生成器的内部状态进行初始化的。

6 具体的伪随机数生成器

6.1 杂乱的方法

用一个程序员都不懂的算法生成，但是这是错误的，不能用于密码技术。因为，周期太短，使用复杂算法所生成的数列大多数都会具有很短的周期（即短数列的不断重复）。另外则是，无法判断所生成的随机数是否具备不可预测性。

6.2 线性同余法

线性同余法（linear congruential method）是一种使用很广泛的伪随机数生成器算法。然而，它并不能用于密码技术。
A、C、M 都是常量，且 A 和 C 需要小于 M。接下来，根据种子 R0 计算下一个伪随机数 R1：
R1 = （A R0 + C） mod M。
当前得到的伪随机数即是下一个伪随机数的种子：
Rn+1 = (A Rn + C) mod M。
但是这具有周期性，而且可以通过上一个种子得到下一个伪随机数。因此不具备不可预测性，不能将线性同余法用于密码技术。
很多伪随机数生成器的库函数都是采用线性同余法编写的。包括 C 语言的库函数 rand。 以及 java 的 java.util.Random 类等。

6.3 单向散列函数法

攻击者要预测下一个伪随机数，需要知道计数器的当前值，以及，破解单向散列函数的单向性。利用了单向散列函数的单向性。

6.4 密码法

密码的机密性是支撑伪随机数生成器不可预测性的基础。

7 对伪随机数生成器的攻击

7.1 对种子进行攻击

7.2 对随机数池进行攻击

一般不会到了需要的时候才当场生成真随机数，而是会事先在一个名为随机数池（random pool）的文件中积累随机比特序列。当密码软件需要伪随机数的种子时，可以从这个随机数池中取出所需长度的随机比特序列来使用。这是不能被攻击所知道的。

8 本章小结

由于密码技术的伪随机数生成器，需要使用单向散列函数和密码等技术来确保不可预测性。

9 小测验

1. 伪随机数的种子需要对攻击者保密。
2. 线性同余法可以作为用于密码的伪随机数生成器。
3. 具备随机性的伪随机数生成器不一定具备不可预测性。

作为区块链存在的主要理由，去中心的定义却含糊不清，这需要澄清一下。

编者按：去中心化是个热词。但是究竟什么是去中心化却存在很多异议。为此比特币改良版在线系统Ethereum的创始人之一Vitalik Buterin从结构、政治和逻辑三个维度剖析了去中心化的含义。

“去中心化”是在加密经济学领域使用最频繁的词之一 ，而且往往被视为区块链存在的全部理由所在，但这个词可能也是定义最糟糕的一个。仅仅为了尝试实现去中心化的这一主要目标，以及为了保护和改善它，已经投入了成千上万小时的研究，数十亿美元的哈希能力。而且当讨论开始出现火药味时，某一协议（或者协议扩展）的支持者把对方提案说成“中心化”作为终极大招使出来实在是太过常见的事情了。

但对于这个词到底是什么含义往往会出现很多的困惑。比方说，我们可以看看下面这个完全毫无帮助但是却不幸地太过常见的示意图：

现在再来看看Quora上面有关“分布式和去中心化的区别”这一问题的两个回答。第一个回答基本上是对上面这张图的鹦鹉学舌，而第二个回答则要大相径庭，声称“分布式意味着并非所有的交易处理都是在同一个地方完成的，”而“去中心化意味着单个实体不能控制完所有的处理。”与此同时，在Ethereum stack exchange上面得票率最高的回答也给出了类似的图解，但是“去中心化”和“分布式”这两个词却交换了位置！显然，这里有做出澄清的必要。

三种类型的去中心化

当大家在讨论软件去中心化的时候，实际上往往有3种不同维度的中心化/去中心化。虽然在一些情况下这些中心化形式往往缺一不可，但通常它们还是彼此相对独立的。这几个维度是：

1. 结构（去）中心化——系统由多少物理计算机组成？该系统可容忍这些计算机多少台同时发生崩溃？
2. 政治（去）中心化——有多少个人或者组织最终控制着组成该系统的那些计算机？
3. 逻辑（去）中心化——该系统展现和维护的界面和数据结构看起来更像是单一的一体式对象呢，还是无定形的一大群？或者用这个问题来启发一下：如果包括提供商和用户在内把你的系统一分为二的话，那两部分是不是还可以继续作为独立单元完全运作？

我们可以把这三个维度用下面这张表来表示：

要指出的是这些设定还是非常粗糙的，还有待商榷。但我们先稍微过一下这几种情况：

• 传统企业是政治中心化（有一个CEO），结构中心化（一个总部）以及逻辑中心化的（并不能真正一分为二）。
• 民法依赖于一个中心化的法律制定实体，而习惯法是基于许多独立判决的基础上制订的。民法仍然有一些结构上的去中心化，因为有很多法庭仍然是由很大的自由裁量权的，但习惯法的自由裁量权更大。这两个都是逻辑中心化的。
• 语言是逻辑去中心化的；Alice和Bob之间讲的英语与Charlie和David之间讲的英语完全不需要一致。语言并不需要一个中心化的基础设施存在，而英语的语法规则也不是由一个人创建或控制的（世界语则是源自Ludwig Zamenhof,的发明，尽管其现在的功能更像是一门无人监管、逐渐演变的活语言）。
• BitTorrent在逻辑上是去中心化的，类似于英语的样子。内容交付网络也类似，但却是被一个公司所控制。
• 区块链是政治去中心化（没人控制区块链）、结构去中心化（没有基础设施性的中心失败点）的，但是在逻辑上是中心化的（有一个公认的状态，整个系统行为就像一个计算机一样）。

很多时候当大家讨论区块链的优点时，他们会描述拥有“一个集中数据库”的便利性；这种中心化是逻辑上的中心化，而且是一种无疑从很多方面来说都是有好处的中心化（尽管IPFS的Juan Benet也希望在可能的情况下推进逻辑去中心化，因为逻辑去中心化系统往往擅长在网络分区中存活，在连接性糟糕的世界各地都工作得很好等；参见Scuttlebot的这篇明确呼吁逻辑去中心化的文章）。

结构中心化往往导致政治中心化，尽管未必会如此——在正式的民主中，政治家以某种实体的治理形式会面和投票，但这种议事厅的维护者最终并不能因此从中获得任何实质性的决策权。而在一个计算化的系统中，结构上去中心化但政治上却是中心化的情况是有可能发生的——如果有一个在线社区出于便利考虑利用了中心化的论坛，但是却没有一个广泛公认的社会契约，比如约定如果论坛所有者出现恶意行为则每个人都会跑到另一个论坛去。

逻辑中心化会导致结构去中心化更加困难，但并非不可能——看看去中心化的舆论网络已被证明有效，但却比维护BitTorrent更加困难就知道了。逻辑中心化也使得政治去中心化更加困难——在逻辑中心化的系统中，你是很难仅仅靠“和平共存”来解决争端的。

去中心化的三个原因

接下来的问题就是为什么去中心化会有用？这通常会有几种观点：

• 可容错——去中心化的系统意外失效的可能性更低，因为它们依靠于许多独立的组件，这些组件不大可能全都失效。

• 抗攻击性——对去中心化系统的攻击、摧毁或者操纵的代价要高很多，因为它们缺乏敏感的中心点，对这些中心点发起攻击的成本要比对周边系统发动攻击的经济规模小得多。

• 抗共谋——去中心化系统的参与者串通行动，以牺牲其他参与者的利益谋取自身利益的难度要大得多，而企业和政府的领导层就可以串通起来谋求自身利益却损害了不那么协调的市民、客户、员工以及普罗大众的利益。

这三种观点都是重要的，也是合理的，但如果你开始思考各自应该采用什么协议时这三种观点都会导致一些有趣但不同的结论。如果感兴趣的可以到原文了解进一步的讨论。

此文转载自：<去中心化的三个维度_36氪>

1 本章概要

SSL（Secure Socket Layer）与TLS(Transport Layer Security)是不同的，TLS 相当于是 SSL 的后续版本。

2 什么是 SSL/TLS

2.1 客户端与服务器

将 Alice 和 Bob 书店的通信过程整理如下图（不使用SSL/TLS）：

Alice 向 Bob 书店发送信用卡号使用 HTTP 来完成。 Alice 输入信用卡号之后按下提交按钮，这时客户端（Web浏览器）就会将信用卡号作为 HTTP 请求发送给服务器。服务器则会将“生成订单”的网页作为 HTTP 响应返回给客户端。

不过，如果直接发送请求的话，信用卡号就很可能被窃听。

2.2 用 SSL/TLS 承载 HTTP

当 Web 浏览器发送信用卡号时，信用卡号的数据会作为客户端请求发送给服务器。使用 SSL/TLS 作为对通信进行加密的协议，然后在此之上承载 HTTP。通过将两种协议进行叠加，我们就可以对 HTTP 的通信（请求和响应）进行加密，从而防止窃听。

2.3 SSL/TLS 的工作

进行安全的通信，我们有几个必须要解决的问题：

1. Alice 的信用卡号和地址在发送到 Bob 书店的过程中不能被窃听。
2. Alice 的信用卡号和地址在发送到 Bob 书店的过程终不能被篡改。
3. 确认通信对方的 Web 服务器是真正的 Bob 书店。

在这里，1 是机密性问题，2 是完整性的问题， 3 则是认证的问题。
要解决这些问题，让我们在密码学家的工具箱中找一找：
要确保机密性，可以使用对称密码。由于对称密码的秘钥不能被攻击者预测，因此我们使用伪随机数生成器来生成秘钥。若要将对称密码的秘钥发送给通信对象，可以使用公钥密码或者 Diffie-Hellman 秘钥交换。
要识别篡改，对数据进行认证，可以使用消息认证码。消息认证码是使用单向散列函数来实现的。
要对通信对象进行认证，可以使用对公钥加上数字签名所生成的证书。
好，工具已经找齐了，下面只要用一个“框架”（framework）将这些工具组合起来就可以了。SSL/TSL 协议其实就扮演了这样一种框架的角色。

2.4 SSL/TLS 也可以保护其它的协议

刚刚我们提到用 SSL/TLS 承载 HTTP 通信，这是因为 HTTP 是一种很常见的协议。其实 SSL/TSL 上面不仅可以承载 HTTP，还可以承载其它很多协议。例如，发送邮件时使用的 SMTP（Simple Mail Transfer Protocol，简单邮件传输协议）和接收邮件时使用的 POP3（Post Office Protocol，邮局协议）都可以用 SSL/TSL 进行承载。在这样的情况下， SSL/TSL 就可以对收发的邮件进行保护。

2.5 密码套件

SSL/TLS 提供了一种密码通信的框架，这意味着 SSL/TSL 中使用的对称密码、公钥密码、数字签名、单向散列函数等技术，都是可以像零件一样进行替换的。也就是说，如果发现现在所使用的某个密码技术存在弱点，那么只要将这一部分进行替换就可以了。
尽管如此，也并不是说所有的组件都可以自由选择。由于实际进行对话的客户端和服务器必须使用相同的密码技术才能进行通信，因此如果选择过于自由，就难以确保整体的兼容性。为此， SSL/TSL 就事先搭配好饭盒一样，规定了一些密码技术的“推荐套餐”，这种推荐套餐称为密码套件（cipher suite）。

2.6 SSL 与 TLS 的区别

SSL（Secure Socket Layer，安全套接层）是 1994 年由网景（Netscape）公司设计的一种协议。而 TLS（Transport Layer Security，传输层安全）是 IETF 在 SSL3.0 的基础上设计的协议，在 1999 年作为 RFC2246 发布的 TLS1.0 ，实际上相当于 SSL3.1 。

3 使用 SSL/TLS 进行通信

下面介绍使用 SSL/TLS 进行通信的步骤。本节内容是基于 TLS1.0 编写的，因此直接写作 TLS。

3.1 层次化的协议

TLS 协议是由“TLS记录协议”（TLS record protocol）和“TLS握手协议”（TLS handshake protocol）这两层协议叠加而成的。位于底层的 TLS记录协议负责进行加密，而位于上层的 TLS握手协议则负责除加密以为的其它各种操作。上层的 TLS握手协议又可以分为 4 个子协议。TLS协议的层次结构如下：

下面简单介绍一下其中各个协议的功能

1.TLS记录协议

TLS记录协议位于 TLS握手协议的下层，是负责使用对称密码对消息进行加密通信的部分。
TLS记录协议中使用了对称密码和消息认证码，但是具体的算法和共享秘钥则是通过握手协议在服务器和客户端之间协商决定的。

2.TLS握手协议

TLS 握手协议分为下列 4 个子协议：握手协议、密码规格变更协议、警告协议和应用数据协议。

2-1 握手协议

握手协议是 TLS握手协议的一部分，负责在客户端和服务器之间协商决定密码算法和共享秘钥。基于证书的认证操作也是在这个协议中完成的。它是 4 个子协议中最复杂的一个。这个协议大致相当于下面这段对话：
客户端：“你好。我能够理解额密码套件由 RSA/3DES，或者 DSS/AES，请问我们使用哪一种密码套件来通信呢？”
服务器：“你好。那么我们用 RSA/3DES 来进行通信吧，这是我的证书。”
在服务器和客户端之间通过握手协议协商一致之后，就会相互发出信号来切换密码。负责发出信号的就是下面要介绍的密码规格变更协议。

2-2 密码规格变更协议

密码规格变更协议是 TLS握手协议的一部分，负责向通信对象传达变更密码方式的信号。简单地说，就跟向对方喊“1、2、3！”差不多。
这个协议所发送的消息，大致相当于下面的对话：
客户端：“好，我们按照刚才的约定切换密码吧。1、2、3！”
当协议中途发生错误时，就会通过下面的警告协议传达给对方。

2-3 警告协议

警告协议是 TLS握手协议的一部分。警告协议负责在发生错误时将错误传达给对方。
这个协议所发送的消息，大致相当于下面的对话：
服务器：“刚才的消息无法正确解密哦！”
如果没有发生错误，则会使用下面的应用数据协议来进行通信。

2-4 应用数据协议

应用数据协议是 TLS 握手协议的一部分。应用数据协议是将 TLS 上面承载的应用数据传达给通信对象的协议。
下面我们按照相同的顺序，更加详细地介绍一下 TLS协议。

3.2 TLS记录协议

TLS记录协议负责消息的压缩、加密以及数据的认证，其处理过程如下：

1. 消息被分割成多个较短的片段（fragment），然后分别对每个片段进行压缩。压缩算法需与通信对象协商决定。
2. 经过压缩的片段会被加上消息认证码，这是为了保证完整性，并进行数据的认证。通过附加消息认证码的 MAC 值，可以识别出篡改。与此同时，为了防止重放攻击，在计算消息认证码时，还加上了片段编号。单向散列函数的算法，以及消息认证码所使用的共享秘钥都需要与通信对象协商决定。
3. 经过压缩的片段再加上消息认证码会一起通过对称密码进行加密。加密使用 CBC模式。
4. 最后，上述经过加密的数据再加上由数据类型、版本号、压缩后的长度组成的报头（header）就是最终的报文数据。其中，数据类型为 TLS记录协议所承载的 4 个子协议的其中之一。

3.3 TLS握手协议

1.握手协议

握手协议是 TLS握手协议的一部分，负责生成共享秘钥以及交换证书。其中，生成共享秘钥是为了进行密码通信，交换证书是为了通信双方互相进行认证。
握手协议这一名乘中的“握手”（handshake），是服务器和客户端在密码通信之前交换一些必要信息这一过程的比喻。
由于握手协议中的信息交换是在没有加密的情况下进行的（即使用“不加密”这一密码套件），也就是说，在这一协议中所收发的所有数据都可能被窃听者 Eve 所窃听，因此，在这一过程中必须使用公钥密码或者 Diffie-Hellman 秘钥交换。

下面我们来详细讲解握手协议中所交换的消息。

2.密码规格变更协议

TLS 的密码规格变更协议（change cipher spec protocol）是 TLS握手协议的一部分，用于密码切换的同步。
那么为什么这个协议不叫密码规格开始协议，而叫密码规格变更协议呢？这是因为即便在密码通信开始之后，客户端和服务器也可以通过重新握手来再次改变密码套件。也就是说，在最开始的时候，客户端和服务器是使用“不加密”这一密码套件进行通信的，因此通信内容没有进行加密。

3.警告协议

TLS 的警告协议（alert protocol）是 TLS握手协议的一部分，用于当发生错误时通知通信对象。当握手协议的过程中产生异常，或者发生消息认证码错误、压缩数据无法解压缩等问题时，会使用该协议。

4.应用数据协议

应用数据协议是 TLS握手协议的一部分，用于和通信对象之间传送应用数据。
当 TLS 承载 HTTP 时，HTTP 的请求和响应就会通过 TLS 的应用数据协议和 TLS 记录协议来进行传送。

3.4 主密码

主密码是 TLS 客户端和服务器之间协商出来的一个密码的数值。这个数值非常重要，TLS 密码通信的机密性和数据的认证全部依靠这个数值。
主密码是根据：预备主密码、客户端随机数、服务器随机数计算出来的。

3.5 TLS 中使用的密码技术小结

4 对 SSL/TLS 的攻击

4.1 对各个密码技术的攻击

针对 SSL/TLS 中使用的各个密码技术的攻击，会直接成为对 SSL/TLS 的攻击。例如，如果能够找到 SSL/TLS 中使用的对称密码的弱点，就相当于找到了 SSL/TLS 通信机密性的弱点。
然而， SSL/TLS 作为框架的特性也正是在这里能够得以体现。 SSL/TLS 并不依赖于某种特定的密码技术，当发现某种对称密码存在弱点时，今后只要选择不包含该对称密码的密码套件就可以了。这就好像一台机器的某个零件损坏时，只要更换这个损坏的零件就可以了。

4.2 对伪随机数生成器的攻击

只要生成伪随机数生成器的种子在可预测范围内，其生成的秘钥是可以被预测的。

4.3 利用证书的时间差进行攻击

SSL/TLS 中，客户端会使用服务器证书对服务器进行认证。在这个过程中，客户端需要使用合法认证机构的公钥对证书所附带的数字签名进行验证。正如第十章所提到那样，如果证书已过期，但是 Web 浏览器没有获取到最新版的信息，这是无法保证通信的安全的。

5 SSL/TLS 用户的注意事项

5.1 不要误解证书的含义

在 SSL/TLS 中，我们能够通过证书对服务器进行认证。然后这里的认证，知识确认了通信对象是经过认证机构确认的服务器，并不能确认是否可以和该通信对象进行安全的在线购物交易。直白点，就是即便对方拥有合法的证书，也不代表你就可以放心地发送信用卡号，因为仅通过 SSL/TLS 是无法确认对方是否在从事信用卡诈骗的。
此外，认证机构所进行的本人身份确认也分为不同的等级，需要仔细确认一下认证机构的业务规则。
为了提高 SSL/TLS 运用的可靠性，一个名为 CA/Brower 论坛的组织制定了 EV SSL 证书（Extended Validation Certificate）规范。

5.2 密码通信之前的数据时不受保护的

SSL/TLS 仅对通信过程中的数据进行保护，而无法保护通信前的的数据。

5.3 密码通信之后的数据时不受保护的

SSL/TLS 也无法保护通信之后的数据。
因此信用卡号不会再通信过程中被第三方获取，而信用卡号在通信之前被偷窥，以及在通信之后，服务器被窃取可能性还是存在的。

6 本章小结

SSL/TLS 是将对称密码、公钥密码、单向散列函数、消息认证码、伪随机数生成器、数字签名等技术相结合来实现安全通信的。通过切换密码套件来使用强度更高的密码算法。

7 小测验

1. 使用 SSL/TLS 可以确保通信的机密性。
2. 在 SSL/TLS 中，使用数字签名技术来认证通信双发的身份。
3. 在 SSL/TLS 中，由于使用了公钥密码或者秘钥交换技术，因此伪随机数生成器的品质低一点也没有关系。
4. 在 SSL/TLS 中，由于公钥是服务器发送的，因此客户端无需持有任何公钥就可以对服务器进行认证。
5. 使用 SSL/TLS 的公司是可信的，因此可以放心地发送信用卡号。

1 本章概要

密码的本质就是将较长得密码——消息，变成较短的密码——秘钥。

2 什么是秘钥

2.1 秘钥就是一个巨大的数字

在使用对称密码、公钥密码、消息认证码、数字签名等密码技术，都需要一个称为秘钥（key）的巨大数字。然后，数字本身的带下并不重要，重要的是秘钥空间的大小，也就是可能出现的秘钥的总数量，因为秘钥空间越大，进行暴力破解就越困难。秘钥空间的大小是由秘钥长度决定的。

1.DES 的秘钥

对称密码 DES 的秘钥的实质长度为 56 比特。
例如，一个 DES 秘钥用二进制可以表示为：
01010001 10100101 10100011 10101010 01101101 10100001 11100011 00100100
用十六进制则可以表示为：
51 EC 4B 12 3D 4A A1
而用十进制则可以表示为：
12309120398102938102983
为了显得专业，将统一使用十六进制。

2.三重 DES 的秘钥

在对称密码三重 DES 中，包括使用两个 DES 秘钥的 DES-EDE2 和使用三个 DES 秘钥的 DES-EDE3 两种方式。
DES-EDE2 的秘钥实际长度为 112 比特。
DES-EDE3 的秘钥实际长度为 168 比特。

3.AES 的秘钥

对称密码 AES 的秘钥长度可以从 128、192和 256 比特中进行选择。

实际长度会更长，因为会加一些用于识别通信错误的校验比特。

2.2 秘钥和明文是等价的

对于窃听密文的 Eve 来说，得到秘钥和得到明文是等价的。即，秘钥和明文是等价的。假设明文具有 100 万元的价值，那么用来加密这段明文的秘钥也就具有 100 万元的价值。

2.3 密码算法与秘钥

信息的机密性不应该依赖于密码算法本身，而是应该依赖于妥善保管的秘钥。这是密码世界的赏识之一。

3 各种不同的秘钥

3.1 对称密码的秘钥与公钥密码的秘钥

在对称密码中，加密和解密使用同一个秘钥。由于发送者和接收者之间需要共享秘钥，因此对称密码又称为共享秘钥密码。

在公钥密码中，加密和解密使用的是不同的秘钥。用于加密的秘钥称为公钥；用于解密的秘钥称为私钥。公钥可以被公开，私钥只能被解密者拥有。

3.2 消息认证码的秘钥与数字签名的秘钥

在消息认证码中，发送者和接收者使用共享的秘钥来进行认证。消息认证码只能由持有合法秘钥的人计算出来。将消息认证码附加在通信报文后面，就可以识别通信内容是否被篡改或伪装。由于“持有合法的秘钥”就是发送者和接收者合法身份的证明，因此消息认证码的秘钥必须对发送者和接收者以外的人保密，否则就会产生篡改和伪装的风险。

在数字签名中，签名的生成和验证使用不同的秘钥。只有持有私钥的本人才能够生成签名，但由于验证签名使用的是公钥，因此任何人都能够验证签名。

3.3 用于确保机密性的秘钥与用于认证的秘钥

对称密码和公钥密码的秘钥都是用于确保机密性的秘钥。如果不知道用于解密的合法秘钥，就无法得知明文的内容。

相对地，消息认证码和数字签名所使用的秘钥，则是用于认证的秘钥。如果不知道合法的秘钥，就无法篡改数据，也无法伪装本人的身份。

3.4 会话秘钥与主秘钥

刚刚我们关注的是秘钥的用途，下面我们来关注一下秘钥被使用的次数。
当我们访问以 https:// 开头的网页时，Web 服务器和浏览器之间会进行基于 SSL/TLS 的加密通信。在这样通信中所使用的秘钥仅限于本次通信的一次性秘钥，下次通信时就不能使用了。像这样每次通信只能使用一次的秘钥称为会话秘钥（session key）。
虽然每次通信都会更会秘钥，但如果用来生成秘钥的伪随机数生成器品质不好，窃听者就有可能预测出下次生成的会话秘钥，这样就会产生内容被破译的风险。
相对于每次通信都更换的会话秘钥，一直被重复使用的秘钥称为主秘钥（master key）。

3.5 用于加密内容的秘钥与用于加密秘钥的秘钥

一般来说，加密的对象使用户直接使用的信息，这样的情况下所使用的秘钥称为 CEK（Contents Encrypting Key，内容加密秘钥）；相对地，用于加密秘钥的秘钥则称为 KEK（Key Encrypting Key，秘钥加密秘钥）。

在很多情况下，之前提到的会话秘钥都是被作为 CEK 使用的，而主秘钥则是被作为 KEK 使用的。

4 秘钥的管理

4.1 生成秘钥

1.用随机数生成秘钥

2.用口令生成秘钥

即人类可以记住的口令（password或passphrase）生成秘钥，但是由字典攻击。

4.2 配送秘钥

在第五章介绍，可以采用事先共享秘钥、使用秘钥分配中心、使用公钥密码等方法。一会将介绍Diffie-Hellman秘钥交换。

4.3 更新秘钥

有一种提高通信机密性的技术被称为秘钥更新（key updating），这种方法就是在使用共享秘钥进行通信的过程中，定期（例如每发送 1000 个字）改变秘钥。

在更新秘钥时，发送者和接收者使用单向散列函数计算当前秘钥的散列值，并将这个散列值用作新的秘钥。简单说，就是用当前秘钥的散列值作为下一个秘钥。
这种防止破译过去的通信内容的机制，称为后向安全（backward security）。

4.4 保存秘钥

由于会话秘钥在通信过程中仅限使用一次，因此我们不需要保存这种秘钥。然而，当秘钥需要重复使用时，就必须要考虑保存秘钥的问题了。

1.人类无法记住秘钥

首先我们必须要理解一个重要的事实，那就是人类是无法记住具有使用长度的秘钥的。

2.对秘钥进行加密的意义

例如，计算机上有 100 万个文件，分别使用不同的秘钥进行加密生成 100 万个密文，结果我们手上就产生了 100 万个秘钥。于是，我们用一个秘钥将这 100 万个秘钥进行加密，那么我们只要保管这一个秘钥就行了。

4.5 作废秘钥

如果秘钥是计算机上的一个文件，那么仅仅删除这个文件是不足以删除秘钥的，此外，很多情况下文件的内容还会残留在计算机的内存中。简而言之，要完全删除秘钥，不但要用到密码软件，还需要在设计计算机系统时对信息安全进行充分的考虑。当然，还要防止秘钥丢失。

5 Diffie-Hellman秘钥交换

5.1 什么是 Diffie-Hellman 秘钥交换

使用这种算法，通信双方仅通过交换一些可以公开的信息就能够生成共享的秘密数字，而这一秘密数字就可以被用作对称密码的秘钥。 IPsec 中就使用了经过改良的 Diffie-Hellman 秘钥交换。

虽然名字叫做“秘钥交换”，但实际上双方并没有真正交换秘钥，而是通过计算机生成出了一个相同的共享秘钥。因此，这种方法也称为 Diffie-Hellman 秘钥协商（Diffie-Hellman key agreement）。

5.2 Diffie-Hellman 秘钥交换的步骤

1.Alice 向 Bob 发送两个质数 P 和 G

P 必须是一个非常大的质数，而 G 则是一个和 P 相关的数，称为生成元。 G 可以是一个较小的数字。 P 和 G 不需要保密。

2.Alice 生成一个随机数 A

A 是一个 1 ~ P-2 之间的整数。这个数是一个只有 Alice 知道的秘密数字，没有必要告诉 Bob ，也不能让 Eve 知道。

3.Bob 生成一个随机数 B

B 是一个 1 ~ P-2 之间的整数。这个数是一个只有 Bob 知道的秘密数字，没有必要告诉 Alice ，也不能让 Eve 知道。

4.Alice 将 G^A mod P 这个数发送给 Bob

这个数让 Eve 知道也没关系

5.Bob 将 G^B mod P 这个数发送给 Alice

这个数让 Eve 知道也没关系

6.Alice 用 Bob 发过来的数计算 A 次方并求 mod P

这个数就是共享秘钥。 (G^B mod P)^A mod P

7.Bob 用 Alice 发过来的数计算 B 次方并求 mod P

这个数就是共享秘钥。 (G^A mod P)^B mod P

8.这样 Alice 和 Bob 得到的值就是相同的

5.3 Eve 能计算出秘钥吗

这是一个离散数学的问题，根据 G^A mod P 的值，以及 G、P 求出 A。非常的困难。

6 基于口令的密码（PBE）

6.1 什么是基于口令的密码

用口令来生成秘钥（KEK）,但只用口令容易遭到字典攻击，那么就用口令和盐共同生成秘钥（KEK），盐可以和加密后的秘钥（CEK）一起保存在磁盘上，而秘钥可以直接丢弃，口令就记在脑子里吧。

6.2 PBE 加密

6.3 PBE 解密

7 本章小结

对秘钥本身做了简单介绍。

8 小测验

1. 由于秘钥只是随机的比特序列，因此被别人知道了也没关系。
2. 私钥是可以公开的。
3. 在 Diffie-Hellman 秘钥交换中，双方可以通过交换一些可以公开的信息生成出共享秘钥。

整部电影感觉有股悲伤的基调，欧维一生皆是不顺，很是平淡，看的确实难受，他是一个好人，却被社会所嫌弃。

他在乎的和在乎他的人都已不在人世，无论是妻子还是好朋友鲁尼（从影片看出，他们是从青年到老年的好朋友了），生活对欧维来说都是如此平淡，每天都面对的是“白痴“。

他孩童时期最高兴的应该是和他父亲一起开车，“这才是人生”，他爸告诉他。这句话，他对那个可爱的小女孩也说了，“这才是人生”。尽管，他很想和自己的孩子说。

我以为应该是个美好结局。

“这才是人生”。

life is not easy. So is suicide.

《En Man Som Heter Ove》

1 本章概要

第五章学习了公钥密码；第九章学习了数字签名。其中公钥都扮演了重要的角色。然后，如果不能判断自己手上的公钥是否合法，就有可能遭到中间人攻击。证书，就是用来对公钥合法性提供证明的技术。

我们先介绍什么是证书，以及证书的应用场景，然后介绍 X.509 证书规范，以及利用证书来进行公钥传输的公钥基础设施（PKI）和认证机构。

2 证书

2.1 什么是证书

公钥证书（Public-Key Certificate，PKC）其实和驾照很相似，里面记有姓名、组织、邮箱、地址等个人信息，以及属于此人的公钥，并由认证机构（Certification Authority、Certifying Authority，CA）施加数字签名。只要看到公钥证书，我们就可以知道认证机构认定该公钥的确属于此人。公钥证书也简称为证书（certificate）。
认证机构就是能够认定“公钥确实属于此人”并能够生成数字签名的个人或者组织。既有国际性组织和政府所设立的组织，也有通过认证服务来盈利的一般企业，此外个人也可以成立认证机构。世界上最有名的认证机构当属 VeriSign 公司。

2.2 证书的应用场景

1. Bob 生成密钥对。这里秘钥既可以 Bob 自己生成，也可以由认证机构代为生成。
2. Bob 在认证机构 Trent 注册自己的公钥。 Bob，需要请认证机构 Trent 对他的公钥加上数字签名（即生成证书）。
   
3. 认证机构 Trent 用自己的私钥对 Bob 的公钥施加数字签名并生成证书。
4. Alice 得到带有认证机构 Trent 的数字签名的 Bob 的公钥（证书）。
5. Alice 使用认证机构 Trent 的公钥验证数字签名，确认 Bob 的公钥的合法性。
6. Alice 用 Bob 的公钥加密消息并发送给 Bob。
7. Bob 用自己的私钥解密密文得到 Alice 的消息。

3 证书标准规范 X.509

1. 签名前的证书——签名对象的信息
2. 数字签名算法——对证书签名时所使用的算法
3. 数字签名——对证书施加的数字签名

4 公钥基础设施（PKI）

4.1 什么是公钥基础设施

公钥基础设施（Public-Key Infrastructure）是为了能够更有效地运用公钥而制定的一些列规范和规格的总称，简称 PKI。它只是一个总称。

4.2 PKI 的组成要素

1. 用户——使用 PKI 的人
2. 认证机构——颁发证书的人
3. 仓库——保存证书的数据

4.3 认证机构的工作

1. 生成密钥对
2. 注册证书
3. 作废证书与 CRL（证书作废清单 Certificate Revocation List）

4.4 证书的层级结构

证书颁发：根CA -> 分公司认证机构 -> 办事处认证机构 -> 用户。
验证证书：根CA -> 分公司认证机构 -> 办事处认证机构 -> 用户。如果连根CA都无法验证说明证书是存在问题的。

5. 对证书的攻击

5.1 在公钥注册之前进行攻击

5.2 注册相似人名进行攻击

5.3 窃取认证机构的私钥进行攻击

5.4 攻击者伪装成认证机构进行攻击

5.5 钻 CRL 的空子进行攻击

Mallory 在晚上入侵 Bob 的电脑，向 Alice 发了邮件。第二天早上， Bob 发现自己电脑被入侵，而且私钥被盗，于是 Bob 赶紧联系认证机构 Trent ，通知自己的公钥被盗，但是已经晚了。同时 Bob 也可以是坏人，利用这个时间差。

6. 关于证书的 Q&A

6.1 为什么需要证书

疑问：我不理解证书的必要性。通过认证机构的证书来获取公钥，和直接获取公钥到底有什么不一样呢？
回答：从认证机构获取公钥，可以降低遭到中间人攻击的风险。因为带有证书的公钥是经过认证机构进行数字签名的，事实上无法被篡改。

6.2 通过自己的方法进行认证是不是更安全

疑问：使用公开的技术就等于为攻击者提供了用于攻击的信息，相比之下，还是使用公司自己开发的保密的认证方法更安全吧？
回答：靠隐蔽式来保证安全是错误的！

6.3 为什么要相信认证机构

？？？

7. 本章小结

从使用证书的场景开始，学习了证书标准规范 X.509、颁发证书的认证机构，以及公钥基础设施（PKI）的相关知识。还介绍了对 PKI 的攻击方法和对策。
无论是数字签名、证书。还是认证机构的层级结构，都不可能在完全不可信的状态下创造出信任关系。这是一种社会的实体问题。

8. 小测验

1. 证书是认证机构将用户的公钥加密后的产物
2. 要确认证书中所包含的公钥是否合法，需要得到认证机构的公钥
3. 世界上颁发的所有证书，沿着认证机构的层级关系都能够找到唯一的根 CA
4. 用户发现自己的私钥泄露之后，需要立刻联系注册相应公钥的认证机构
5. 用户需要定期从认证机构获取 CRL

1 羊妈妈的认证

大灰狼把黑色的爪子伸进门缝，说道：
“我是你们的妈妈，快快开门吧！”
七只小羊回答道：
“不是不是，妈妈的手是白色的，你的手的黑色的，你不是我们的妈妈！”
听了小羊的话，大灰狼把它的爪子染成了白色，于是小羊们就被大灰狼的白爪子给骗了，便打开了门。
这是因为小羊们用来认证的“白色的手”是大灰狼也能够模仿出来的。
如果有一种“只有羊妈妈才能生成的信息”，那就可以实现更可靠的认证了吧。

2 本章概要

数字签名是一种将相当于现实世界中的盖章、签字的功能在计算机世界中实现的技术。使用数字签名可以识别篡改和伪装，还可以防止否认。

3 数字签名

3.1 Alice 的借条

假设 Alice 需要向 Bob 借 100 万元。不过 Alice 和 Bob 离得很远，无法直接见面。通过银行汇款， Alice 可以立刻从 Bob 那里收到钱，但是 Alice 的借条应该怎样发送给 Bob 呢？挂号信寄过去，但是会花费时间，能不能用电子邮件来发送借条呢？比如：
“Bob，我向你借款 100 万元。”————Alice。
显然，Bob 看到这封邮件也不会轻易相信，因为电子邮件容易被伪造也可能被篡改，或者事后 Alice 可以以“我不知道这张借条”为理由来否认。

3.2 从消息认证码到数字签名

1. 消息认证码的局限性

第八章介绍的消息认证码由局限性，即，无法防止否认，以及无法向第三方证明消息是对方发的。

2. 通过数字签名解决问题

假设 Alice 使用的秘钥是一个只有 Alice 自己才知道的私钥。当 Alice 发送消息时，她用私钥生成一个“签名”。相对的，接收者 Bob 则使用一个和 Alice 不同的秘钥对签名进行验证。使用 Bob 的秘钥无法根据消息生成签名，但是用 Bob 的秘钥却可以对 Alice 所计算的签名进行验证，也就是说可以知道这个签名是否是通过 Alice 的秘钥计算出来的。
实际上，这种看似神奇的技术，早就已经问世了，这就是数字签名（digital signature）。

3.3 签名的生成和验证

在数字签名技术中，出现了下面两种行为：

• 生成消息签名的行为
• 验证消息签名的行为

生成消息签名：由消息发送者 Alice 来完成。表明“我认可该消息的内容”。
验证数字签名：由消息接收者 Bob 来完成或者需要验证消息的第三方来完成，即验证者 Victor。

Alice 使用“签名秘钥”来生成消息的签名，而 Bob 和 Victor 则使用“验证秘钥”来验证消息的签名。数字签名对签名秘钥和验证秘钥进行了区分，使用验证秘钥是无法生成签名的。这一点非常重要。此外，签名秘钥只能由签名的人持有，而验证秘钥则是任何需要验证签名的人都可以持有。
这里和第五章的公钥密码很相似。实际上，数字签名和公钥密码有着非常紧密的联系，简而言之，数字签名就是通过将公钥密码“反过来用”而实现的。

3.4 公钥密码与数字签名

4 数字签名的方法

我们来介绍两种生成和验证数字签名的方法：

1. 直接对消息签名的方法
2. 对消息的散列值签名的方法

后者虽然复杂，但实际中我们一般都使用这种方法。

4.1 直接对消息签名的方法

发送者 Alice 要对消息签名，而接收者 Bob 要对签名进行验证。
Alice 需要事先生成一个包括公钥和私钥的密钥对，而需要验证签名 签名的 Bob 则需要得到 Alice 公钥。过程如下：

1. Alice 用自己的私钥对消息进行加密。
2. Alice 将消息和签名发送给 Bob。
3. Bob 用 Alice 的公钥对收到的签名进行解密。如果不是 Alice 的私钥加密的密文，则无法用 Alice 的公钥正确解密。
4. Bob 将签名解密后得到的消息与 Alice 直接发送的消息进行对比。

4.2 对消息的散列值签名的方法

与对消息签名的不同是， 这里的消息变成了消息的散列值。流程参考上图。

5 对数字签名的疑问

5.1 密文为什么能作为签名使用

疑问：为什么密文能够具备签名的意义呢？
解答：数字签名是 利用了“没有私钥的人事实上无法生成使用该私钥所生成的密文”这一性质来实现的。并非为了保证机密性，而是代表只有持有该秘钥的人才能够生成的信息。
这样的信息一般称为认证符号（authenticator），消息认证码也是认证符号的一种，数字签名也是一样。

5.2 数字签名不能保证机密性吗

疑问：从流程图看到，消息没有经过加密就发送了，这样不就无法保证消息的机密性了吗？
解答：的确，数字签名的作用本来就不是保证机密性。关于密码和签名的组合方法，将在第十三章 PGP 详解。

5.3 这种签名可以随意复制吗

疑问：数字签名貌似可以轻易复制出相同内容，那还能用作签名吗？
解答：签名重要的是，特定的签名者与特定的消息绑定在了一起这一事实。无论将签名复制了多少份，“是谁对这条消息进行了签名”这一事实是不会发生任何改变的。签名可以被复制，但这并不代表签名会失去意义。

5.4 消息内容会不不会任意修改

疑问：消息和签名两者都是可以任意修改的，这样的签名还有意义吗？
解答：数字签名所要实现的并不是防止修改，而是识别修改。修改没问题，但验证签名会失败。

5.5 删除签名也无法“作废合同”吗

疑问：带有数字签名的借据只是计算机文件，将其删除也无法保证确实已经作废，因为不知道其它地方是否还留有副本。无法作废的签名是不是非常不方便呢？
解答：我们可以在消息中声明该消息的有效期并加上数字签名，例如公钥的证书就属于这种情况，将在第十章详解。

5.6 如何防止否认

严格来说，如果数字签名的声称这说“我的私钥被别人窃取了”，也是有可能进行否认的，将在第十章探讨。

5.7 数字签名真的能够代替签名吗

不能代替，而是共存。

6 数字签名的应用实例

6.1 安全信息公告

一些信息安全方面的组织会在其网站上发布一些关于安全漏洞的警告，那么这么警告是否真的是该组织所发布的呢？因此，人们可以通过公钥 可以排除有人恶意伪装成该组织来发布假消息的风险。

6.2 软件下载

保证网络下载的软件是否被篡改过。

6.3 公钥证书

在验证数字签名时我们需要合法的公钥，那么怎么才能知道自己得到的公钥是否合法呢？我们可以将公钥当作消息，对它加上数字签名。像这样对公钥施加数字签名所得到的就是公钥证书，将在第十章详解。

6.4 SSL/TLS

SSL/TLS 在认证服务器身份是否合法时会使用服务器证书，它就是加上了数字签名的服务器公钥。相对的，服务器为了对客户端（用户）进行认证也会使用客户端证书。将在第十四章详解。

7 通过 RSA 实现数字签名

7.1 用 RSA 生成签名

签名 = 消息 ^ D mod N

这里所使用的 D 和 N 就是签名者的私钥。

7.2 用 RSA 验证签名

由签名求得的消息 = 签名 ^ E mod N

这里所使用的 E 和 N 就是签名者的公钥。

7.3 具体实践

假设密钥对：
公钥：E = 5; N = 323;
私钥：D = 29; N = 323;

1.生成签名

消息^D mod N = 123^29 mod 323 = 157
得到签名是 157，向接收者发送的内容为：(123，157)。

2.验证签名

签名^E mod N = 157^5 mod 323 = 123
得到的消息 123 与发送者直接发送过来的消息 123 是一致的，因此签名验证成功。

8 其它的数字签名

1. EIGamal 方式：利用了在 mod N 中求离散对数的困难度。
2. DSA。
3. Rabin 方式：利用了在 mod N 中其平方根的困难度。

9 对数字签名的攻击

9.1 中间人攻击

9.2 对单向散列函数的攻击

数字签名中所使用的单向散列函数必须具有抗碰撞性，否则攻击者就可以生成另外一条不同的消息，使其与签名所绑定的消息具有相同的散列值。

9.3 利用数字签名攻击公钥密码

将密文以邮件方式发送给可以解密者，诱导其帮忙解密。（博主认为，这属于社会工程学范畴）

10 各种密码技术的对比

10.1 消息认证码与数字签名

10.2 混合密码系统与散列值签名

在混合密码系统中，消息本身是用对称密码加密的，而只有对称密码的秘钥是用公钥密码加密的，即在这里对称密码的秘钥就相当于消息。
另一方面，数字签名中也使用了同样的方法，即将消息本身输入单向散列函数求散列值，然后再对散列值进行签名，在这里散列值就相当于消息。
即：对称密码的秘钥是机密性的精华，单向散列函数的散列值是完整性的精华。

11 数字签名无法解决的问题

用数字签名既可以识别出篡改和伪装，还可以防止否认。也就是说，我们同时实现了确认消息的完整性、进行认证以及防止否认。
然而，要正确使用数字签名，有一个大前提，那就是用于验证签名的公钥必须属于真正的发送者。
现在由陷入了一个死循环，数字签名是用来识别消息篡改、伪装以及否认的，但是为此我们又必须从没有被伪装的发送者得到没有被篡改的公钥才行。
为了能够确认自己得到的公钥是否合法，我们需要使用证书。所谓证书，就是讲公钥当作一条消息，由一个可信的第三方对其签名后所得到的公钥。

但是这只是把问题转移了。为了对证书上施加的数字签名进行校验，我们必定需要另一个公钥，那么如何才能构建一个可信的数字签名链条呢？又由谁来颁发可信的证书呢？到这一步，我们就已经踏入了社会学的领域。我们需要让公钥以及数字签名技术成为一种社会性的基础设施，即公钥基础设施（Public Key Intrastructure），简称 PKI，关于证书和 PKI 将在第十章详解。

12 本章小结

本章介绍了，如何逆向使用公钥密码来实现数字签名，并使用 RSA 具体实践了数字签名的生成和验证。此外讨论了数字签名的攻击方法以及数字签名与消息认证码之间的关系。
通过数字签名可以识别篡改和伪装，还可以防止否认，但前提是用于验证严明的发送者的公钥没有被伪造。

13 小测验

1. 要验证数字签名，需要使用签名者的私钥。
2. RSA 可以用作数字签名算法。
3. 使用数字签名可以保护消息的机密性，不用担心被窃听。

1 本章概要

使用消息认证码可以确认自己受到的消息是否就是发送者的本意，也就是说，使用消息认证码可以判断消息是否被篡改，以及是否有人伪装成发送者发送了该消息。
消息认证码是密码学家工具箱中 6 个重要的工具之一。这 6 个重要工具分别是：对称密码、公钥密码、单向散列函数、消息认证码、数字签名和伪随机数生成器。

2 消息认证码

2.1 汇款请求是正确的吗

我们需要关注汇款请求的“完整性”和“认证”这两个性质。即汇款的内容以及汇款请求是否是正确的人发送的请求。
消息的完整性（integrity），就是我们在第七章介绍过的“消息没有被篡改”这一性质，完整性也叫一致性。如果消息完整，也就意味着消息没有被篡改。
消息的认证（authentication）指的是“消息来自正确的发送者”这一性质，如果能够确认汇款请求确实来自 Alice，就相当于对消息进行了认证，也就意味着消息不是其他人伪装成发送者所发出的。
本章中介绍的消息认证码，我们就可以同时识别出篡改和伪装，也就是既可以确认消息的完整性，也可以进行认证。

2.2 什么是消息认证码

消息认证码（message authentication code）是一种确认完整性并进行认证的技术，简称为 MAC。
消息认证码的输入包括任意长度的消息和一个发送者和接收者之间共享的秘钥，它可以输出固定长度的数据，这个数据称为 MAC 值。
根据任意长度的消息输出固定长度的数据，这一点和单向散列函数很类似。但是单向散列函数中计算散列值不需要秘钥，而消息认证码则需要使用发送者和接收者之间共享的秘钥。
要计算 MAC 必须持有共享秘钥，没有共享秘钥的人就无法计算 MAC 值，消息认证码正是利用这一性质来完成认证的。此外，和单向散列函数的散列值一样，哪怕消息中发生 1 比特的变化， MAC 值也会产生变化，消息认证码正是利用这一性质来确认完整性的。

后面我们会讲到，消息认证码有很多实现方法，大家可以暂且这样理解：消息认证码是一种与秘钥相关联的单向散列函数。

2.3 消息认证码的使用步骤

以 Alice 银行和 Bob 银行的故事为例，来讲解一下消息认证码的使用步骤。

1. 发送者 Alice 与接收者 Bob 事先共享秘钥。
2. 发送者 Alice 根据汇款请求消息计算 MAC 值（使用共享秘钥）。
3. 发送者 Alice 将汇款请求消息和 MAC 值两者发送给接收者 Bob。
4. 接收者 Bob 根据接收到的汇款请求消息计算 MAC 值（使用共享秘钥）
5. 接收者 Bob 将自己计算的 MAC 值与从 Alice 处收到的 MAC 值进行对比。
6. 如果两个 MAC 值一致，则接收者 Bob 就可以断定汇款请求的确来自 Alice（认证成功）；否则认证失败。

2.4 消息认证码的秘钥配送问题

发送者和接收者需要共享秘钥，这一点和我们在第三章中介绍的对称密码很相似。实际上，对称密码的秘钥配送问题在消息认证码中也同样会发生。要解决秘钥配送问题，我们需要像对称密码一样使用一些共享秘钥的方法，例如公钥密码、Diffie-Hellman 秘钥交换、秘钥分配中心，或者使用其它安全的方式发送秘钥等。

3 消息认证码的应用实例

3.1 SWIFT

SWIFT 的全称是 Society for Worldwide Interbank Financial Telecommunication（环球银行金融电信协会），其目的是为国际银行间的交易保驾护航。银行和银行之间是通过 SWIFT 来传递交易消息的。而为了确认消息的完整性以及对消息进行验证， SWIFT 中使用了消息认证码。
在使用公钥密码进行秘钥交换之前，消息认证码所使用的共享秘钥都是由人来进行配送的。

3.2 IPsec

IPsec 是对互联网基本通信协议——IP协议（Internet Protocol）增加安全性的一种方式。在 IPsec 中，对通信内容的认证和完整性校验都是采用消息认证码来完成的。

3.3 SSL/TLS

SSL/TLS 中对通信内容的认证和完整性校验也使用了消息认证码，将在第十四章详解。

4 消息认证码的实现方法

4.1 使用单向散列函数实现

使用 SHA-1、MD5 之类的单向散列函数可以实现消息认证码，其中一种实现方法称为 HMAC，具体将在下节介绍。

4.2 使用分组密码实现

使用 DES、AES 之类的分组密码可以实现消息认证码。
将分组密码的秘钥作为消息认证码的共享秘钥来使用。

4.3 其它实现方法

使用流密码和公钥密码等也可以实现消息认证码。

5 HMAC 的详细介绍

5.1 什么是 HMAC

HMAC 是一种使用单向散列函数来构造消息认证码的方法，其中的 HMAC 的 H 就是 Hash 的意思。
HMAC 中所使用的单向散列函数并不仅限于一种，任何高强度的单向散列函数都可以被用于 HMAC，如果将来设计出新的单向散列函数，同样可以使用。
使用 SHA-1、MD5、RIPEMD-160 所构造的 HMAC，分别称为 HMAC-SHA-1、HMAC-MD5 和 HMAC-RIPEMD。

5.2 HMAC 的步骤

1.秘钥填充

如果秘钥比单向散列函数的分组长度要短，就需要在末尾填充 0 ，直到其长度达到单向散列函数的分组长度为止。
如果秘钥比分组长度要长，则要用单向散列函数求出秘钥的散列值，然后将这个散列值用作 HMAC 的秘钥。 HMAC-SHA-1 的分组长度为 516 比特。

2.填充后的秘钥与 ipad 的 XOR

将填充后的秘钥与被称为 ipad 的比特序列进行 XOR 运算。ipad 是将 001100110 这一比特序列（即 16 进制的 36）不断循环反复直到达到分组长度所形成的比特序列，其中 ipad 的 i 是 inner 的意思。
XOR 运算所得到的值，就是一个和单向散列函数的分组长度相同，且和秘钥相关的比特序列。这里我们将这个比特序列称为 ipadkey。

3.与消息组合

随后，将 ipadkey 与消息进行组合，也就是将和秘钥相关的比特序列（ipadkey）附加在消息的开头。

4.计算散列值

将第三步的结果输入单向散列函数，并计算出散列值。

5.填充后的秘钥与 opad 的 XOR

将填充后的秘钥与被称为 opad 的比特序列进行 XOR 运算。opad 是将 01011100 这一比特序列（即 16 禁止的 5C）不断循环反复直到达到分组长度所形成的比特序列，其中 opad 的 o 是 outer 的意思。
XOR 运算所得到的结果也是一个和单向散列函数的分组长度相同，且和秘钥相关的比特序列。我们将这个比特序列称为 opadkey。

6. 与散列值组合

将第四步的散列值拼在 opadkey 后面。

7.计算散列值

将第六步的结果输入单向散列函数，并计算出散列值，这个散列值就是最终的 MAC 值。
通过上述流程我们可以看出，最后得到的 MAC 值，一定是一个和输入的消息以及秘钥都相关的长度固定的比特序列。

6 对消息认证码的攻击

6.1 重放攻击

Mallory 想到可以通过将事先保存的正确 MAC 值不断重放来发动攻击，如果这种攻击成功的话，就可以让 100 万元滚雪球到 1 亿元。

1. Mallory 到 Alice 银行向自己在 Bob 银行中的账户 汇款 100 万元。于是 Alice 银行为该汇款请求消息计算出正确的 MAC 值，然后将 MAC 和消息一起发送给 Bob 银行。
2. Bob 银行用收到的消息自行计算 MAC 值，并与收到的 MAC 值进行对比，由于两个值相等，因此 Bob 银行向 Mallory 的账户汇款 100 万元。
3. Mallory 窃听了 Alice 银行发给 Bob 银行的汇款请求消息以及 MAC 值，并保存在自己的计算机中。
4. Mallory 将刚刚保存下来的汇款请求消息以及 MAC 值再次发给 Bob 银行。
5. Bob 银行重复第二步，于是给 Mallory 的账户汇款 100 万元。
6. Mallory 继续重复第四步。
7. Bob 银行重复第五步。

有几种方法可以防御重放攻击。

1.序号

约定每次都对发送的消息赋予一个递增的序号，并且在计算 MAC 值时将序号也包含在消息中。这样，由于 Mallory 无法计算序号递增之后的 MAC 值，因此就可以防御重放攻击。这个方法有效，但是对每个通信对象都需要记录最后一个消息的序号。

2.时间戳

约定在发送消息时包含当前的时间，但是发送者和接收者的时钟必须一致，而且考虑到通信的延迟，必须在时间的判断上留下缓冲，于是多多少少还是会存在可以进行重放攻击的空间。

3.nonce

在通信之前，接收者先向发送者发送一个一次性的随机数，这个随机数一般称为 nonce。发送者在消息中包含这个 nonce 并计算 MAC 值。由于每次通信时 nonce 的值都会发生变化，因此无法进行重放攻击。虽然有效，但通信的数据量会有所增加。

6.2 密码推测攻击

和对单向散列函数的攻击一样，对消息认证码也可以进行暴力破解以及生日攻击（7.6.2节）。
对于消息认证码来说，应保证不能根据 MAC 值推测出通信双方所使用的秘钥。如果 Mallory 能够从 MAC 值反算出秘钥，就可以进行篡改、伪装等攻击。例如 HMAC 中就是利用单向散列函数的单向性和抗碰撞性来保证无法根据 MAC 值推测出秘钥的。
此外，在生成消息认证码所使用的秘钥，必须用高强度的伪随机数生成器。

7 消息认证码无法解决的问题

7.1 对第三方证明

假设 Bob 想要向第三方验证着 Victor 证明这条消息的却是 Alice 发送的，但是用消息认证码无法进行这样的证明，因为，Victor 要校验 MAC 值，就需要知道 Alice 和 Bob 之间共享的秘钥，假设 Bob 将秘钥告诉 Victor，但是 Victor 有理由相信，这条消息有可能是 Bob 伪装 Alice 发送的。使用第九章的数字签名就可以实现对第三方的证明。

7.2 防止否认

假设 Bob 收到了包含 MAC 值得消息，这个 MAC 值是用 Alice 和 Bob 共享的秘钥计算出来的，因此 Bob 能够判断这条消息的确来自 Alice。但是， Alice 可以说“这条消息是 Bob 自己编的吧”，说白了，就是 Alice 和 Bob 吵起来了。
即便 Bob 拿 MAC 值举证，Victor 也无法判断 Alice 和 Bob 谁才是正确的，也就是说，用消息认证码无法防止否认（nonrepudiation）。这种情况，数字签名同样可以实现防止否认。

8 本章小结

本章介绍的消息认证码，是对消息进行认证并确认其完整性的技术，通过使用发送者和接收者之间共享的秘钥，就可以识别出是否存在伪装和篡改行为。
其可以使用单向散列函数和对称密码等技术来实现，本章重点介绍了通过单向散列函数来实现的 HMAC。
消息认证码的缺点在于，由于发送者和接收者共享相同的秘钥，因此会产生无法对第三方证明以及无法否认等问题。
下一章的数字签名可以解决这些问题。

9 小测验

1. 使用消息认证码能够确保消息的机密性。注：消息本身的机密性不是由消息认证码决定的。
2. 使用消息认证码能够识别出篡改行为。
3. 使用消息认证码需要发送者和接收者之间共享的秘钥。
4. 使用消息认证码能够防止否认。

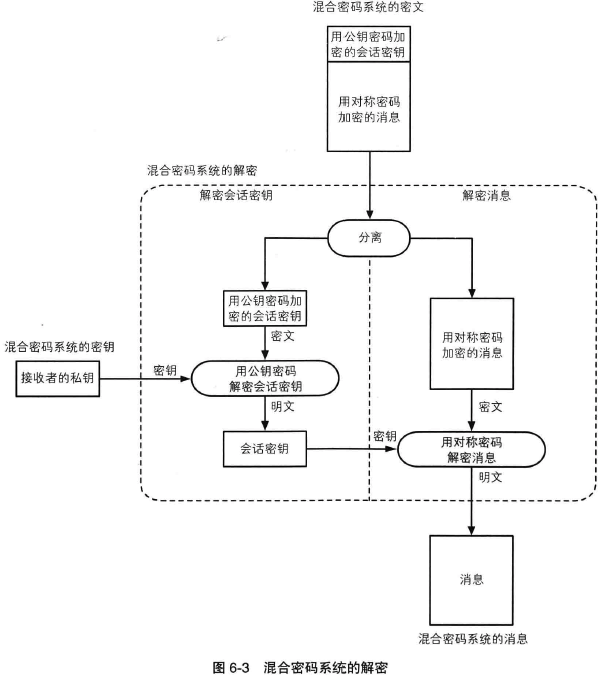
1 本章概要

针对计算机所处理的消息，有时候我们也需要用到“指纹”。当需要比较两条消息是否一致时，我们不必直接对比消息本身的内容，只要对比它们的“指纹”即可。
本章中，使用单向散列函数就可以获取消息的“指纹”，通过对比“指纹”，就能够知道两条消息是否一致。
我们将详细介绍现在使用非常广泛的 SHA-1 单向散列函数，并思考对单向散列函数的攻击方法。

2 什么是单向散列函数

2.1 这个文件是不是真的呢

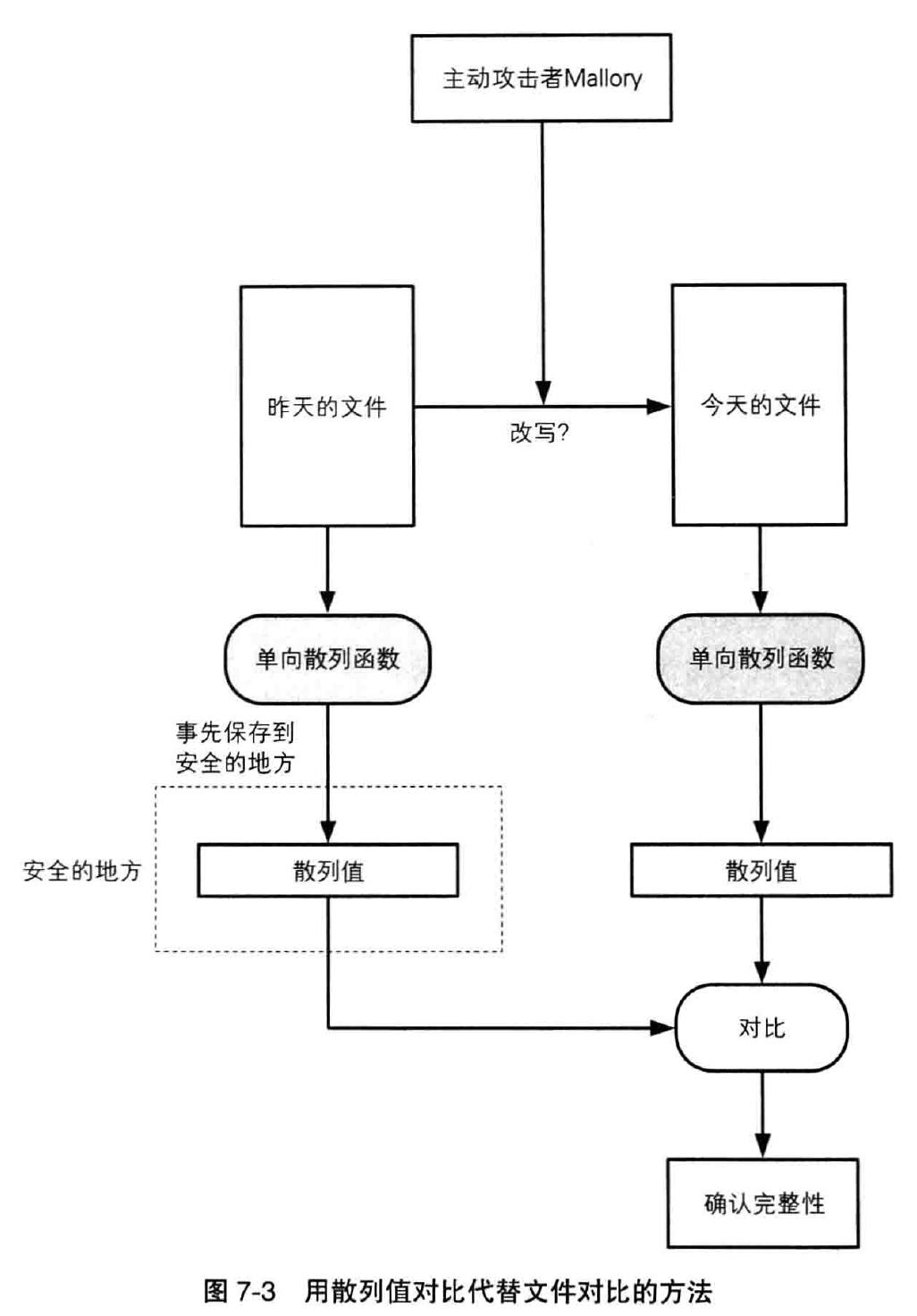
Alice 终于完成了一个软件开发，接下来只要把文件从 Alice 的硬盘中拷贝到 CD 上就可以了。不过，把文件写到 CD 上非常耗时， Alice 已经很累了，她决定今天晚上早上回家休息，明天再继续弄。
第二天， Alice 来到公司准备把文件写入 CD ，但她忽然产生了这样的疑问：
“这个文件和我昨天晚上生成的文件是一样的吗？”
Alice 的疑问是这样的——会不会有人操作 Alice 的计算机，将文件改写了呢？也有可能通过网络入侵 Alice 的计算机。或者，也许 Alice 的计算机感染了病毒，造成文件被篡改……在这里，我们姑且把篡改文件的这个主体称为“主动攻击者 Mallory”。总而言之，Alice 需要知道从昨天到今天这段时间内， Mallor有 是否篡改了文件的内容。

也就是说，Alice 需要确定自己的文件的完整性（integrity）。

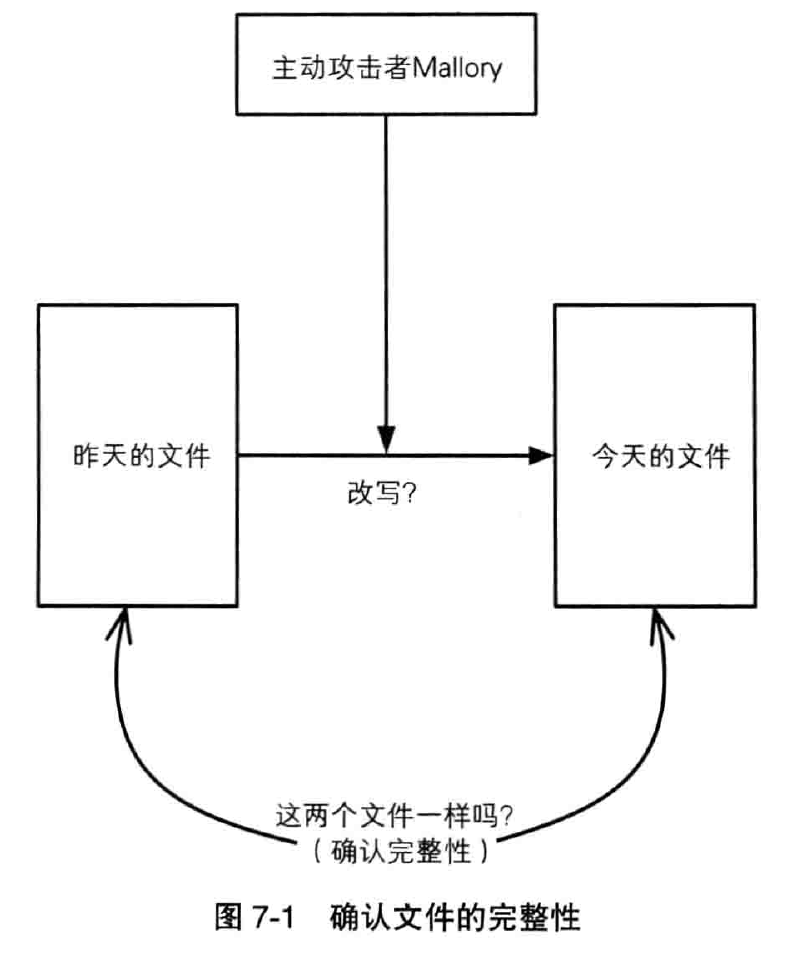
稍微想一想我们就能找一种确认文件完整性的简单方法——在回家之前先把文件拷贝到一个安全的地方保存，第二天在用这个文件工作之前，先将其和事先保存的文件进行对比就可以了。如果两者一致，那就说明文件没有被篡改。
不过，下图这种确认完整性的方法，其实是毫无意义的。因为如果可以事先把文件保存在一个安全的地方，那根本就不需要确认完整性，直接用事先保存的文件来工作不就行了吗？

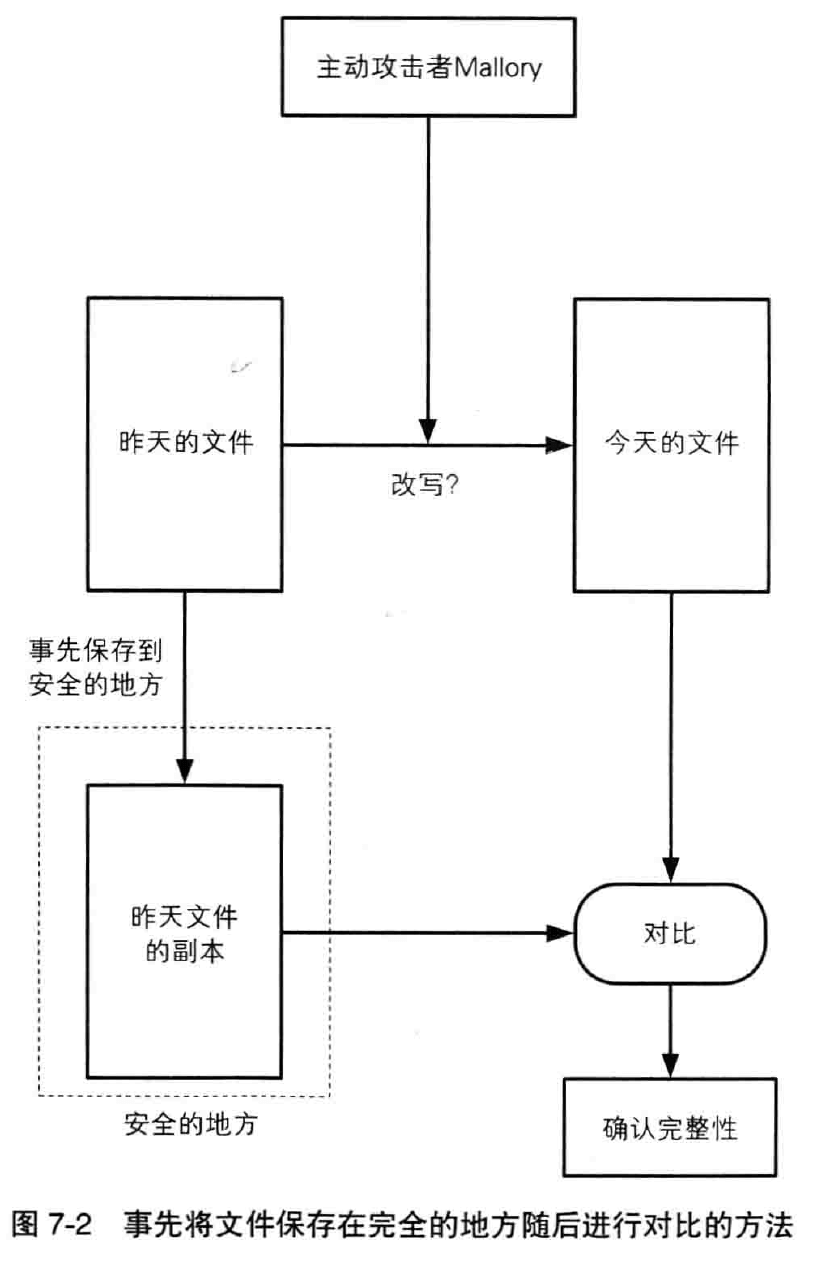
这里还存在一个效率问题。如果需 需要确认完整性的文件非常巨大，那么文件的拷贝、保存以及比较都将非常耗时。
我们能不能获取到 Alice 所生成的文件的“指纹”呢？如果我们不需要对整个巨大的文件进行对比，只需要对比一个较小的指纹就能够检查完整性的话，那该多方便：

本章要介绍的单向散列函数，就是一种采集文件指纹的技术。单向散列函数所生成的散列值，就相当于消息的指纹。

2.2 什么是单向散列函数

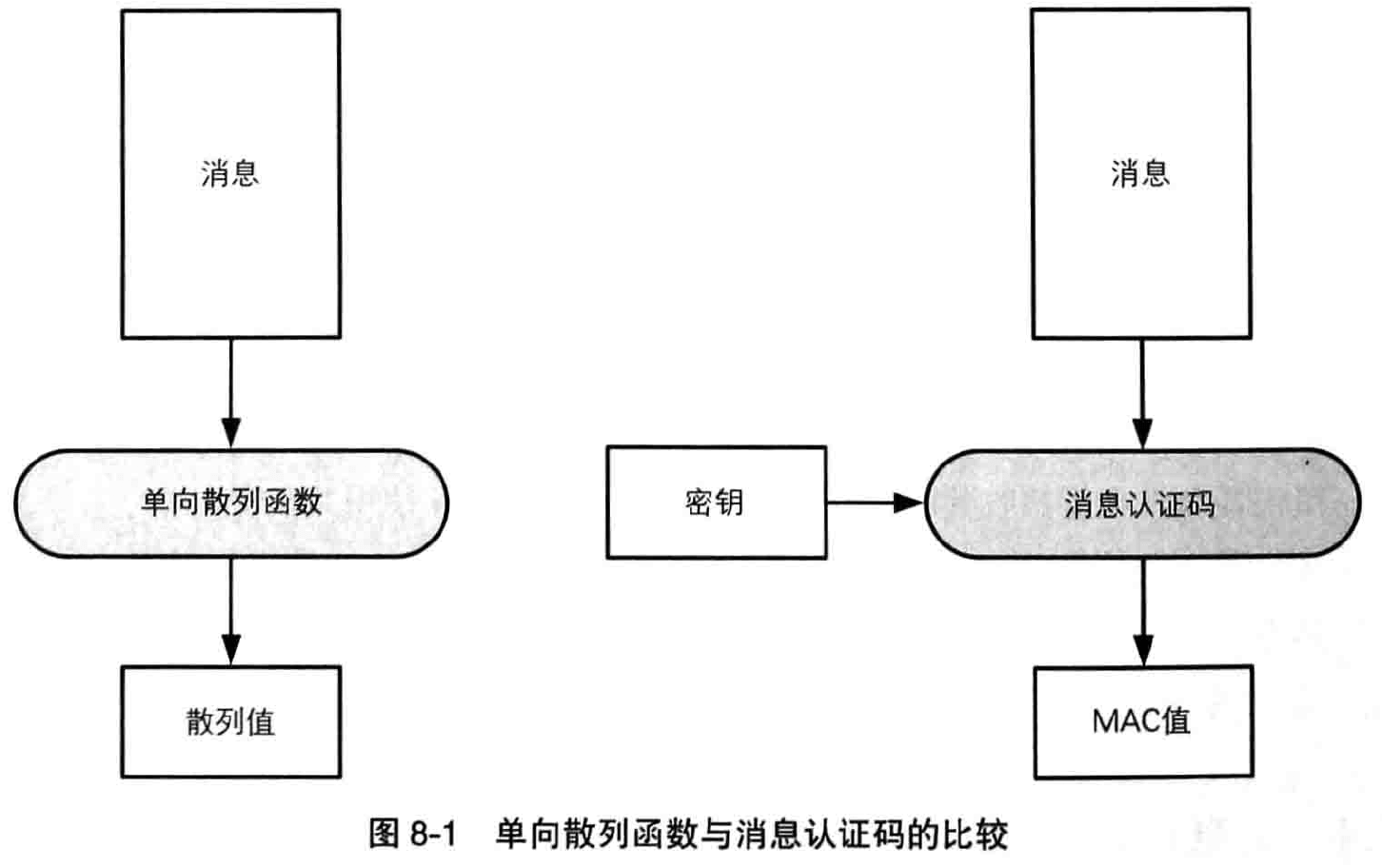
单向散列函数（one-way hash function）有一个输入和一个输出，其中输入称为消息（message），输出称为散列值（hash value）。单向散列函数可以根据消息的内容计算出散列值，而散列值就可以被用来检查消息的完整性。

这里的消息可以是任何形式的消息，图像、声音、视频。因为无论任何消息，单向散列函数都会将它作为单纯的比特序列来处理，即根据比特序列计算出散列值。
散列值的长度和消息的长度无关。以 SHA-1 单向散列函数为例，它所计算出的散列值的长度永远是 160 比特（20字节）。

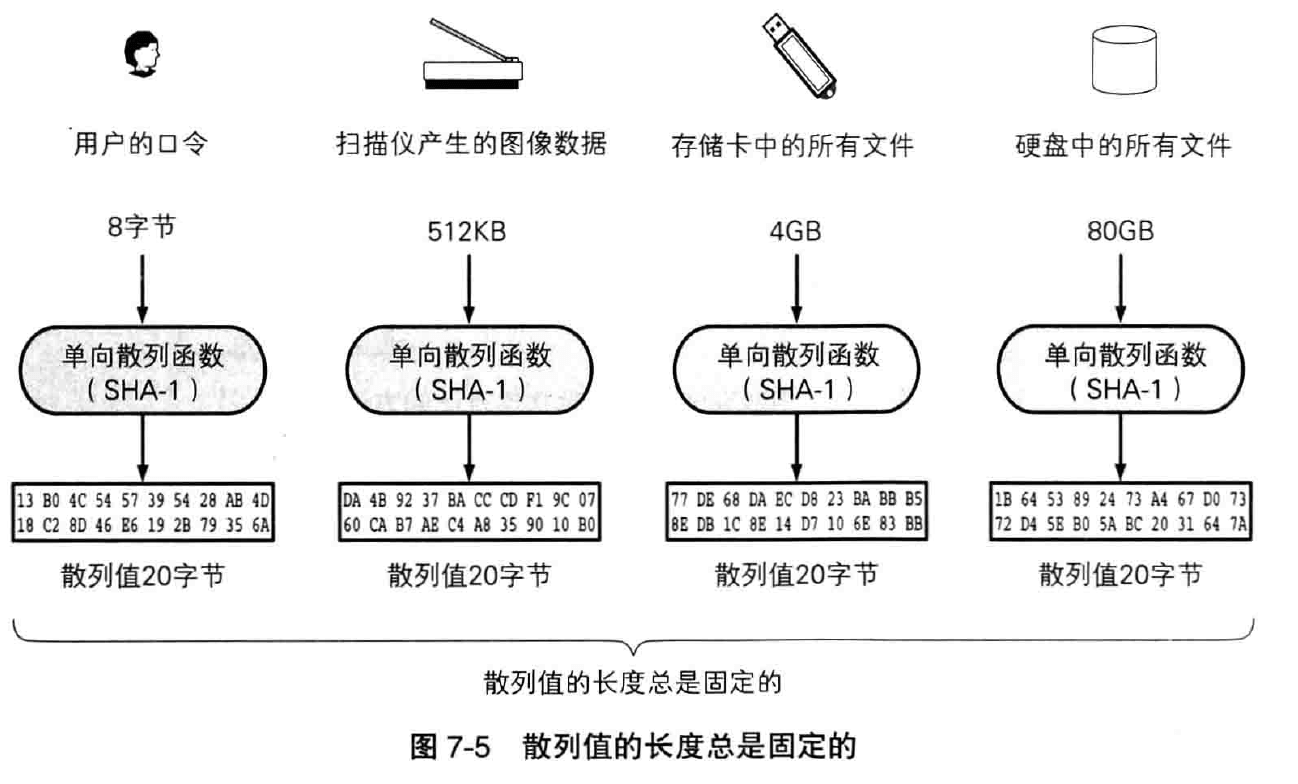
由于散列值很短，因此很容易处理和使用。

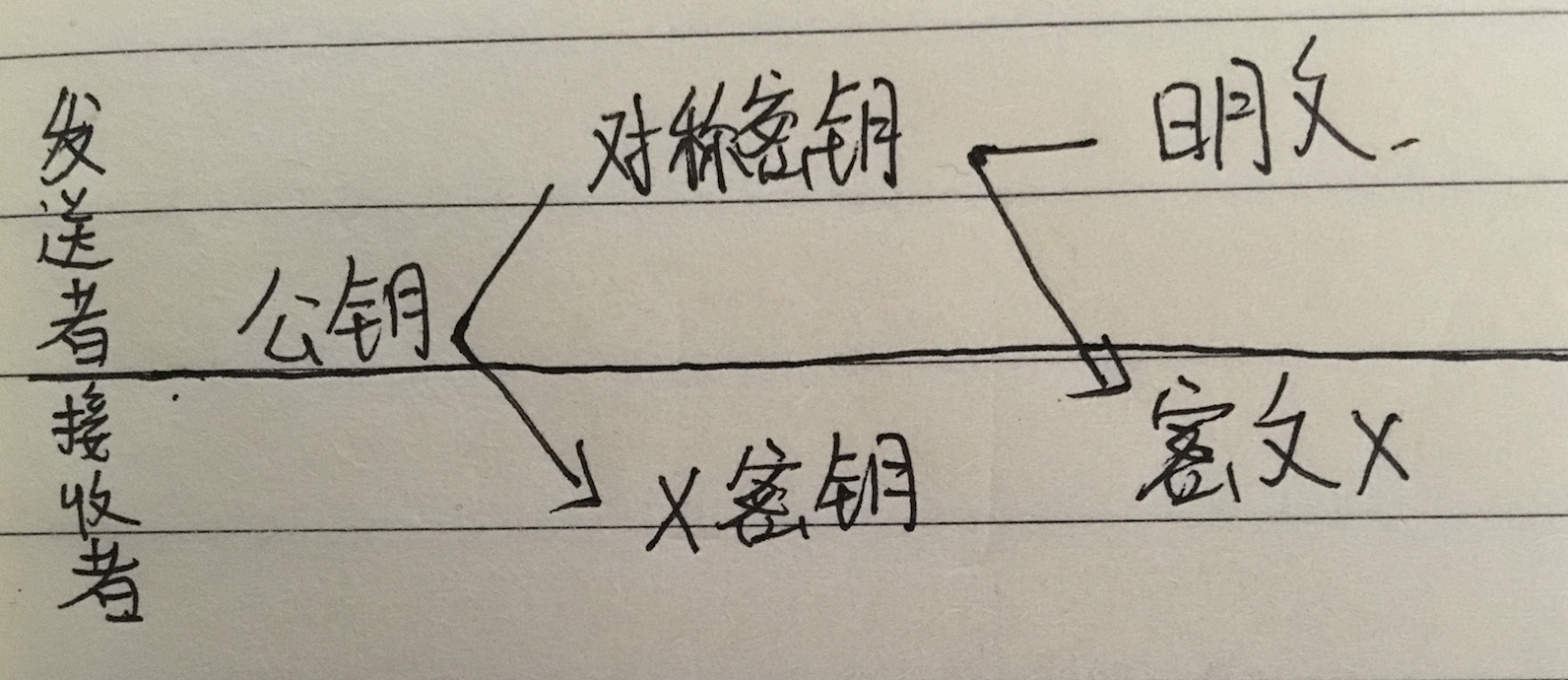
回家之前，Alice 用单向散列函数计算文件的散列值：
35 36 37 38 39 A1 D2 F4 J5 5B 9J 35 36 37 38 39 A1 D2 F4 J5
单向散列函数所输出的散列值的长度是固定的（在这个例子中是 20 字节），无论 Alice 的文件大小是多大，散列值永远都是 20 字节（160比特）。Alice 可以将这个值打印出来，保存，或者拿回家藏在枕头下面~
第二天早上，Alice 再次计算硬盘中文件的散列值，如果再次计算出的散列值和昨晚的散列值相同，就可以判断这个文件是真的，否则就是不一样的。

2.3 单向散列函数的性质

1. 根据任意长度的消息计算出固定长度的散列值

2.能够快速计算出散列值

3.消息不同散列值也不同

如果单向散列函数计算出的散列值没有发生变化，那么消息很容易就会被篡改，这个单向散列函数也就无法被用于完整性的检查。两个不同的消息产生同一个散列值的情况称为碰撞（collision）。如果要将单向散列函数用于完整性的检查，则需要确保在事实上不可能被认为地发现碰撞。
难以发现碰撞的性质称为抗碰撞性（collision resistance）。密码技术中所使用的单向散列函数，都需要具备抗碰撞性。
我们以 Alice 用单向散列函数来检查文件完整性的场景为例，现在，我们假设 Alice 所使用的单向散列函数不具备抗碰撞性。
Alice 在回家之前得到了散列值，Alice 在睡觉的时候，Mallory 入侵了 Alice 的计算机，并改写了 Alice 的文件。

由于假设 Alice 的单向散列函数不具备抗碰撞性，因此 Mallory 能够找到一种改写文件的方法，使得改写后文件的散列值不会发生变化，因此 Alice 将 Mallory 改写后的文件写入了 CD。

这里所说的抗碰撞性，指的是难以找到另外一条具备特定散列值的消息。当给定某条消息的散列值时，单向散列函数必须确保要找到和该条消息具有相同散列值的另外一条消息是非常困难的。这一性质称为弱抗碰撞性。单向散列函数都必须具备弱抗碰撞性。

和弱抗碰撞性相对的，还有强抗碰撞性。所谓强抗碰撞性，是指要找到散列值相同的两条不同的消息是非常困难的这一性质。在这里，散列值可以是任意值。

密码技术中所使用的单向散列函数，不仅要具备弱抗碰撞性，还必须具备强抗碰撞性。

4. 具备单向性

2.4 关于术语

单向散列函数也称为消息摘要函数（message digest function）、哈希函数或者杂凑函数。
输入单向散列函数的消息也称为原像（pre-image）。
单向散列函数输出的散列值也称为消息摘要（message digest）或者指纹（fingerprint）**。
完整性也称为一致性。
“散列”的英文 “hash” 一词，原意是“斧子”，后来被引申为“剁碎的肉末”。单向散列函数的作用，实际上就是将很长的消息剁碎，然后再混合成固定长度的散列值。

3 单向散列函数的实际应用

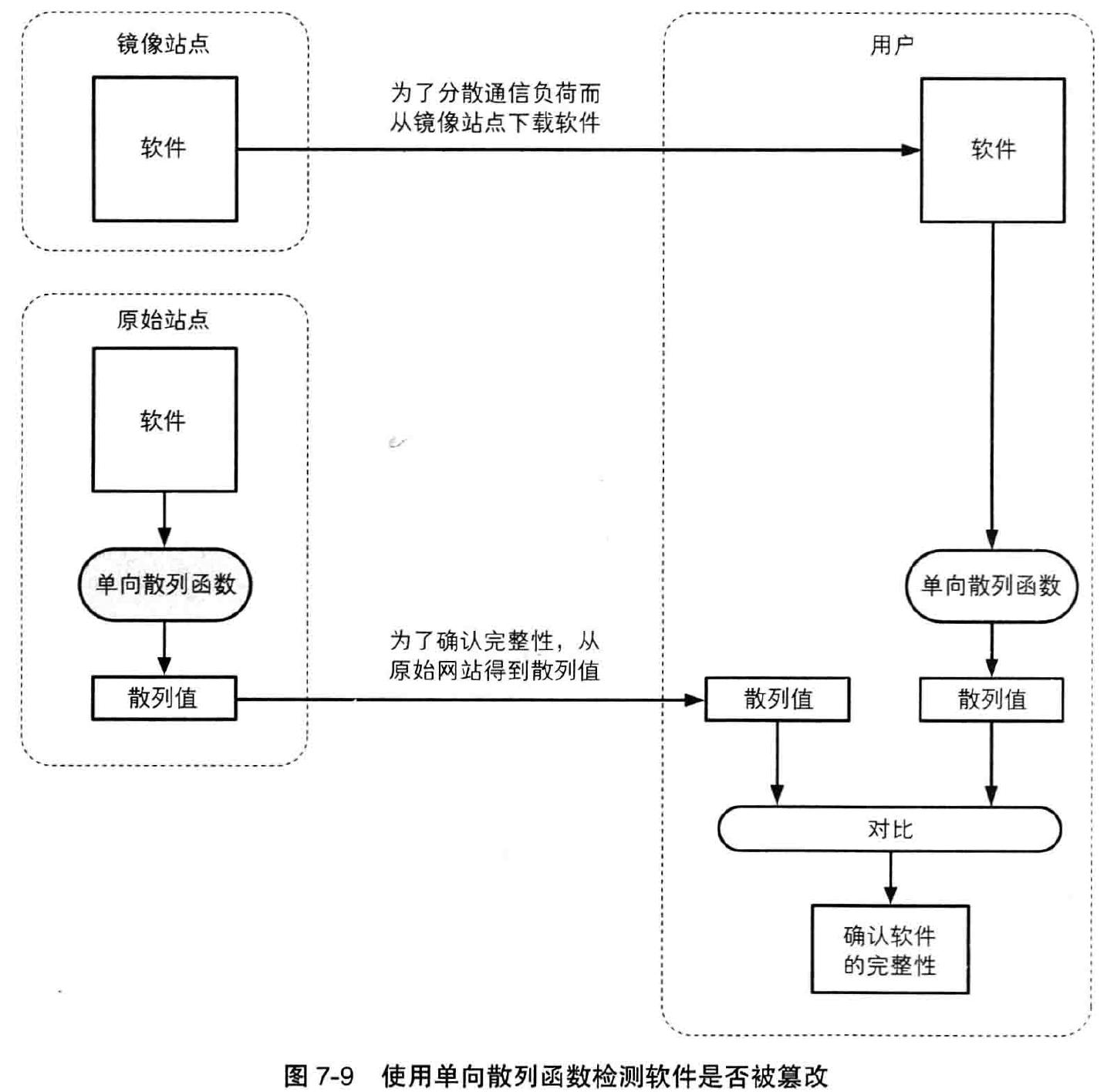
3.1 检测软件是否被篡改

3.2 基于口令的加密

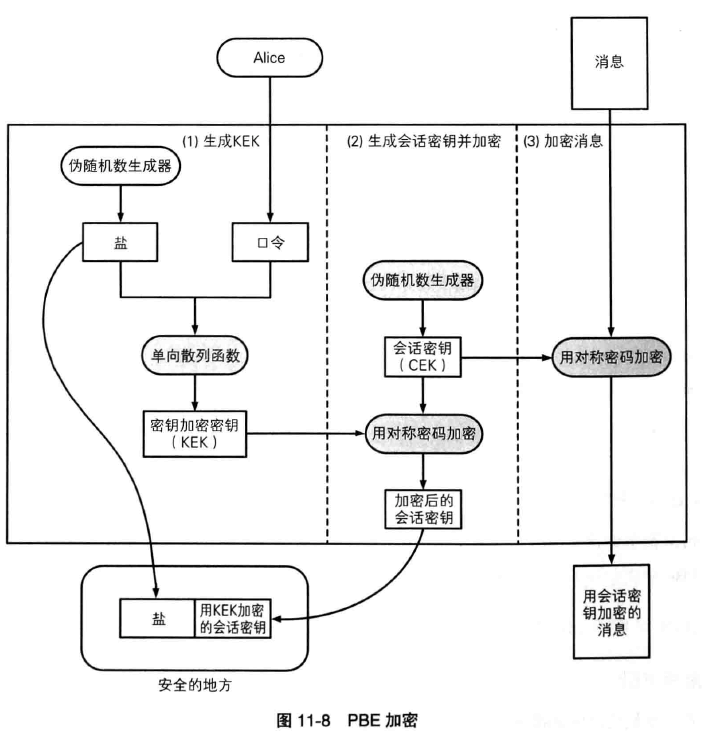
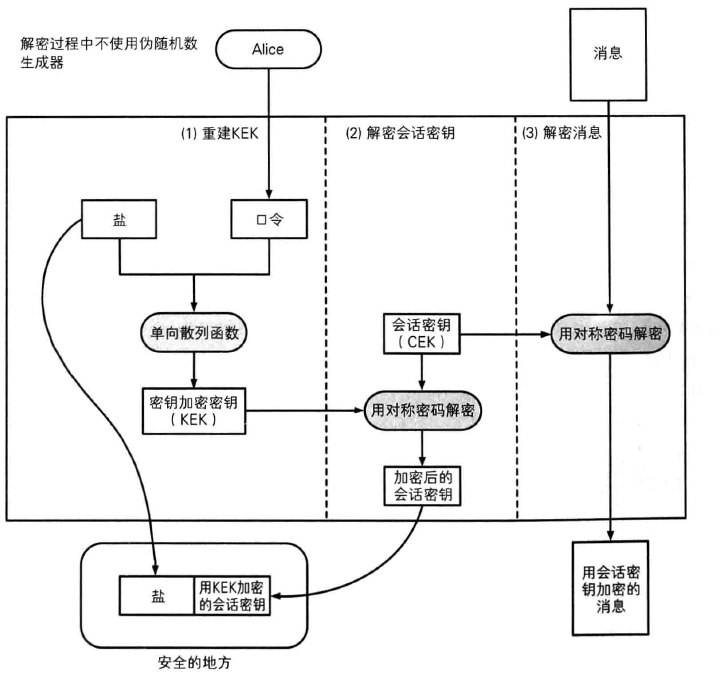
单向散列函数也被用于基于口令的加密（Password Based Encryption，PBE）。
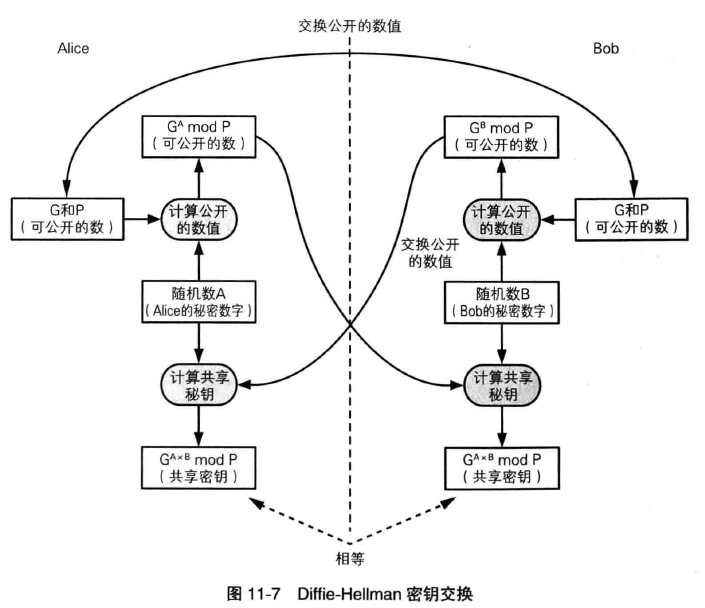
PBE 的原理是将口令和盐（salt，通过伪随机数生成器产生的随机值）混合后计算起散列值，然后将这个散列值用作加密的秘钥。通过这样的方法能够防御针对口令的字典攻击，将在第十一章详解。

3.3 消息认证码

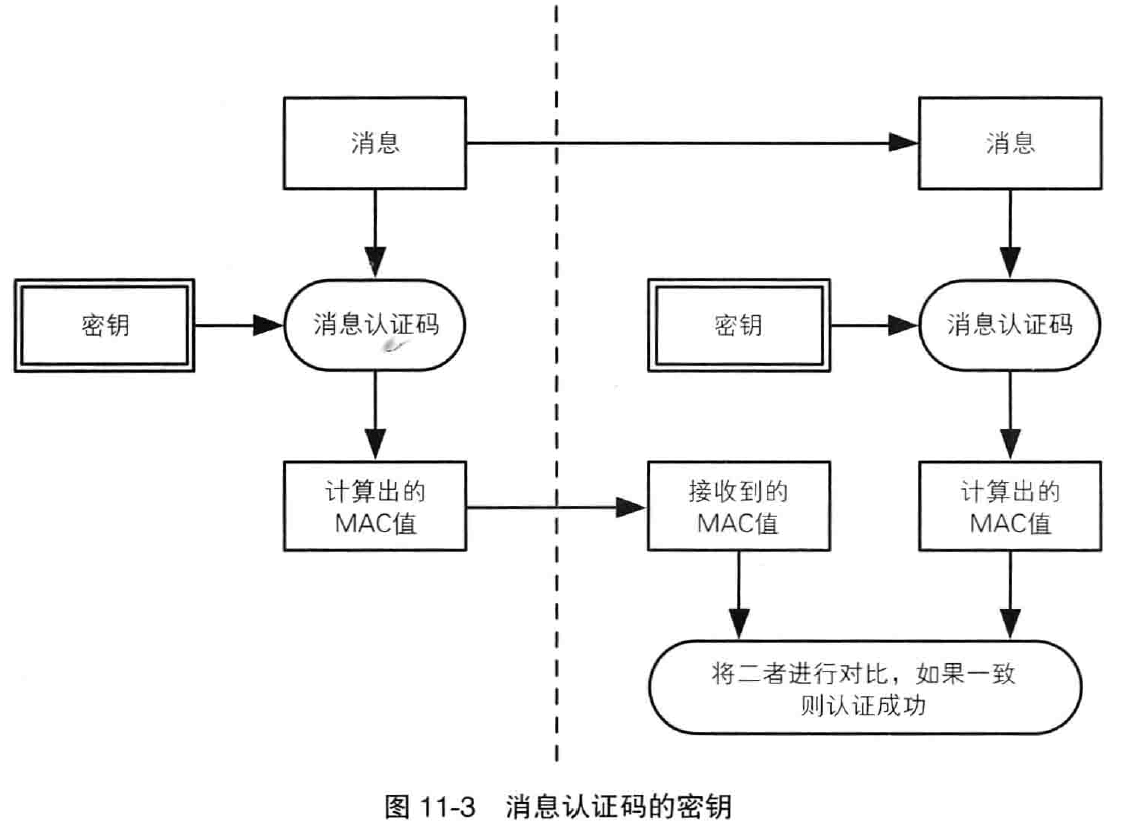
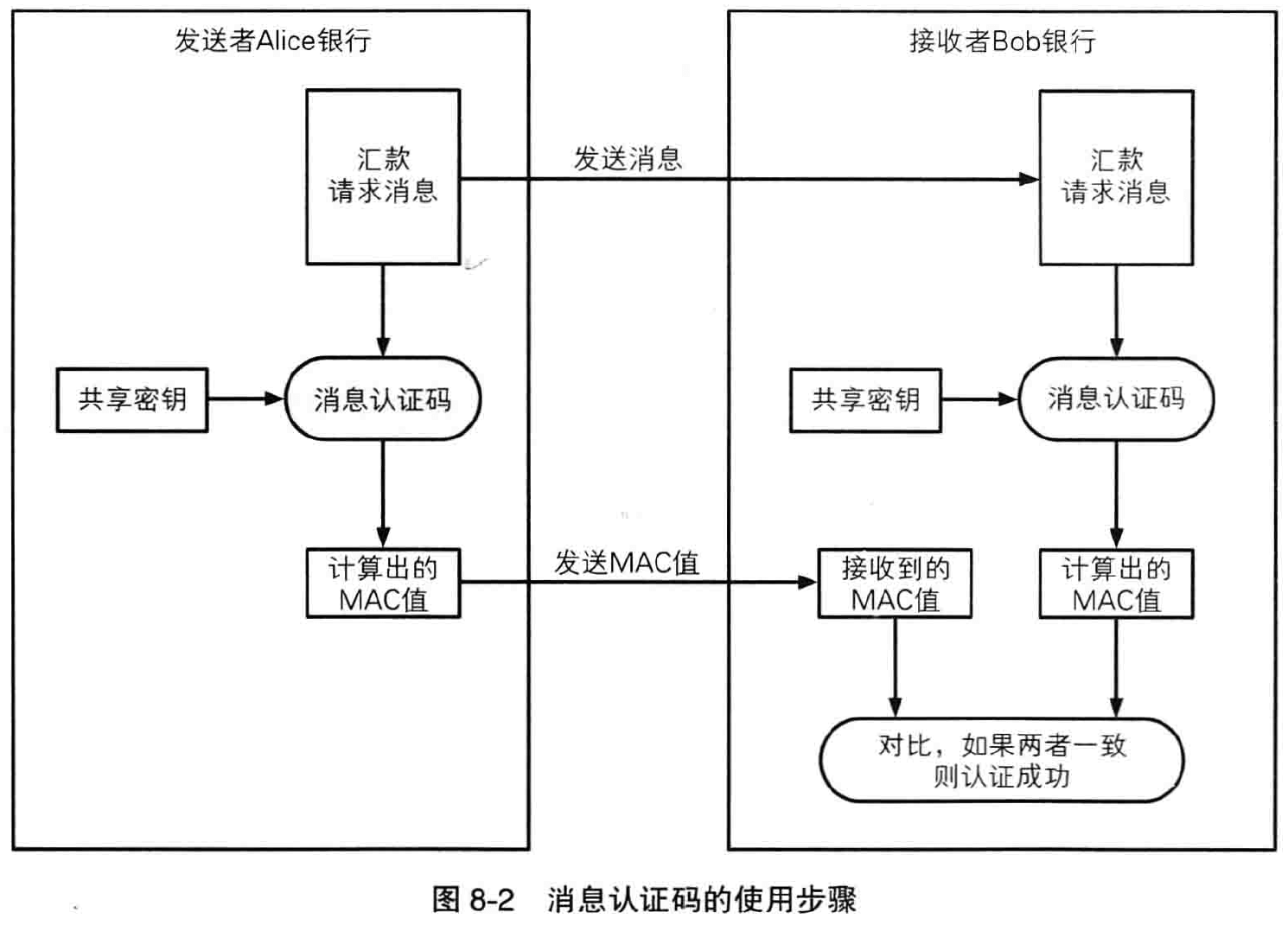
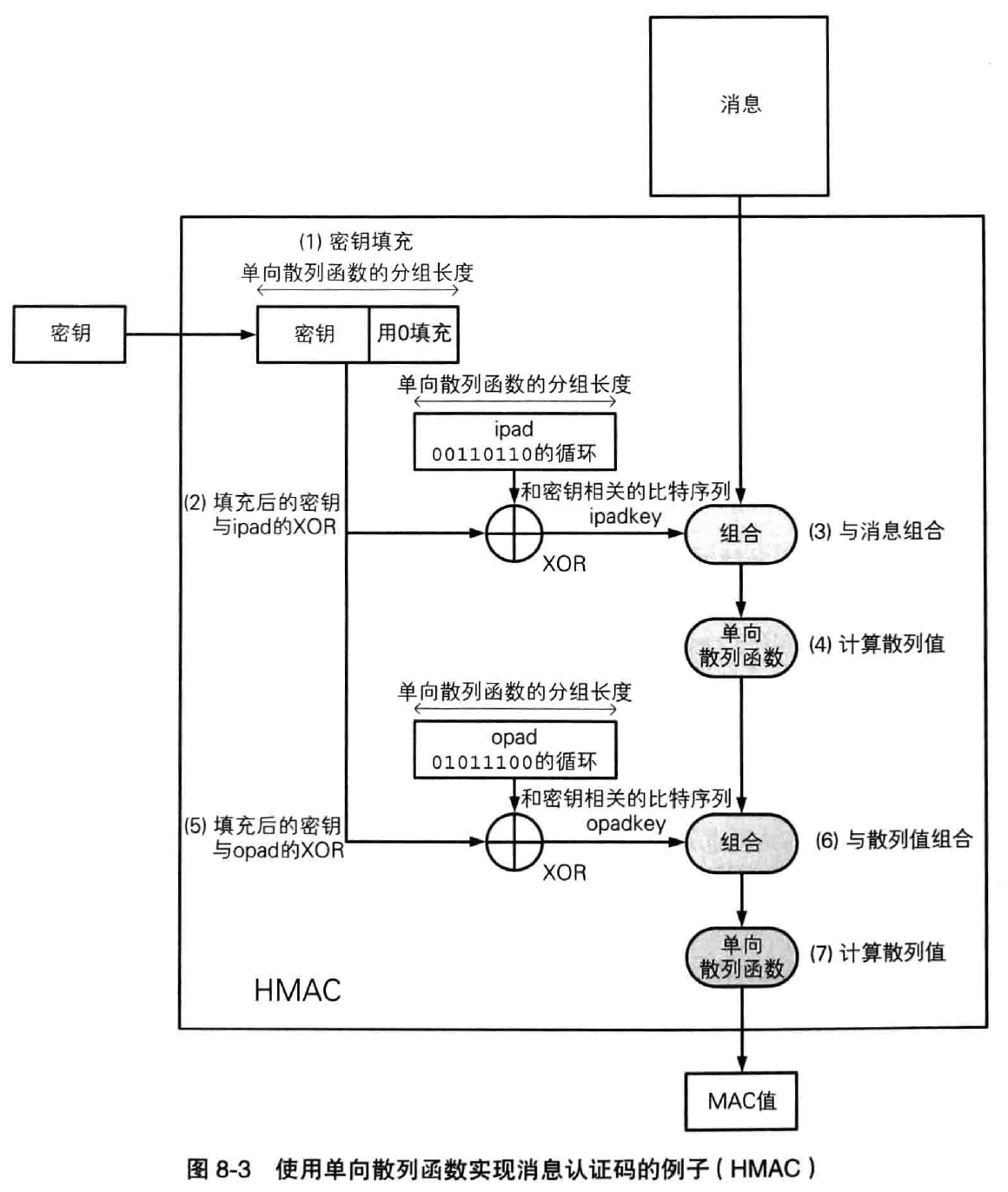
使用单向散列函数可以构造消息认证码。
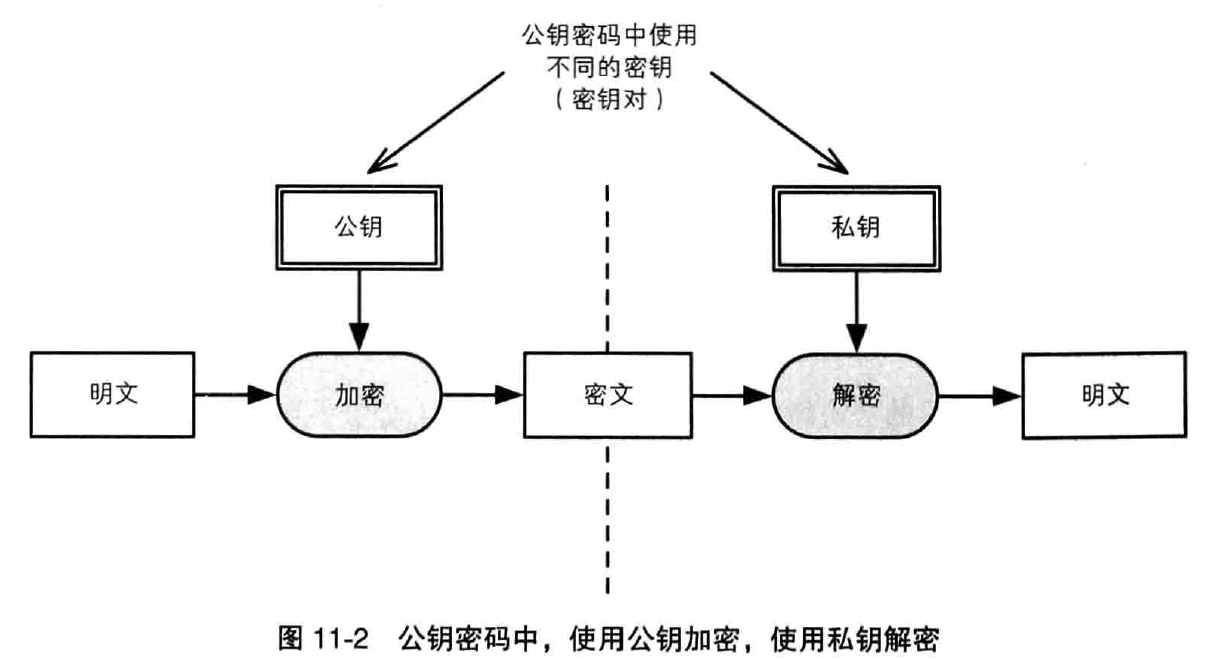
消息认证码是将“发送者和消息接收者之间的共享秘钥”和“消息”进行混合后计算出的散列值，使用消息认证码可以检测并防止通信过程中的错误、篡改以及伪装。
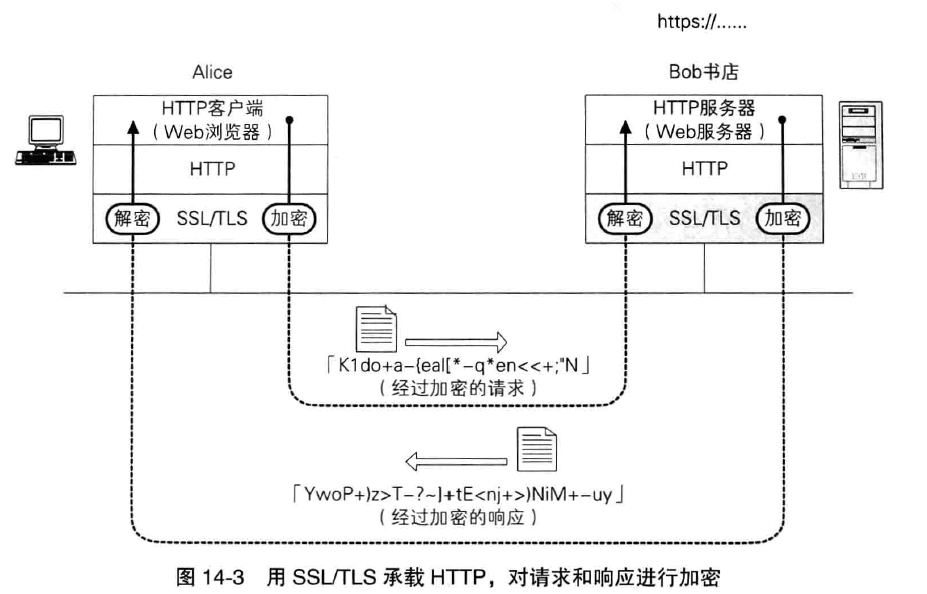
消息认证码在 SSL/TLS 中也得到了运用，将在第十四章详解。

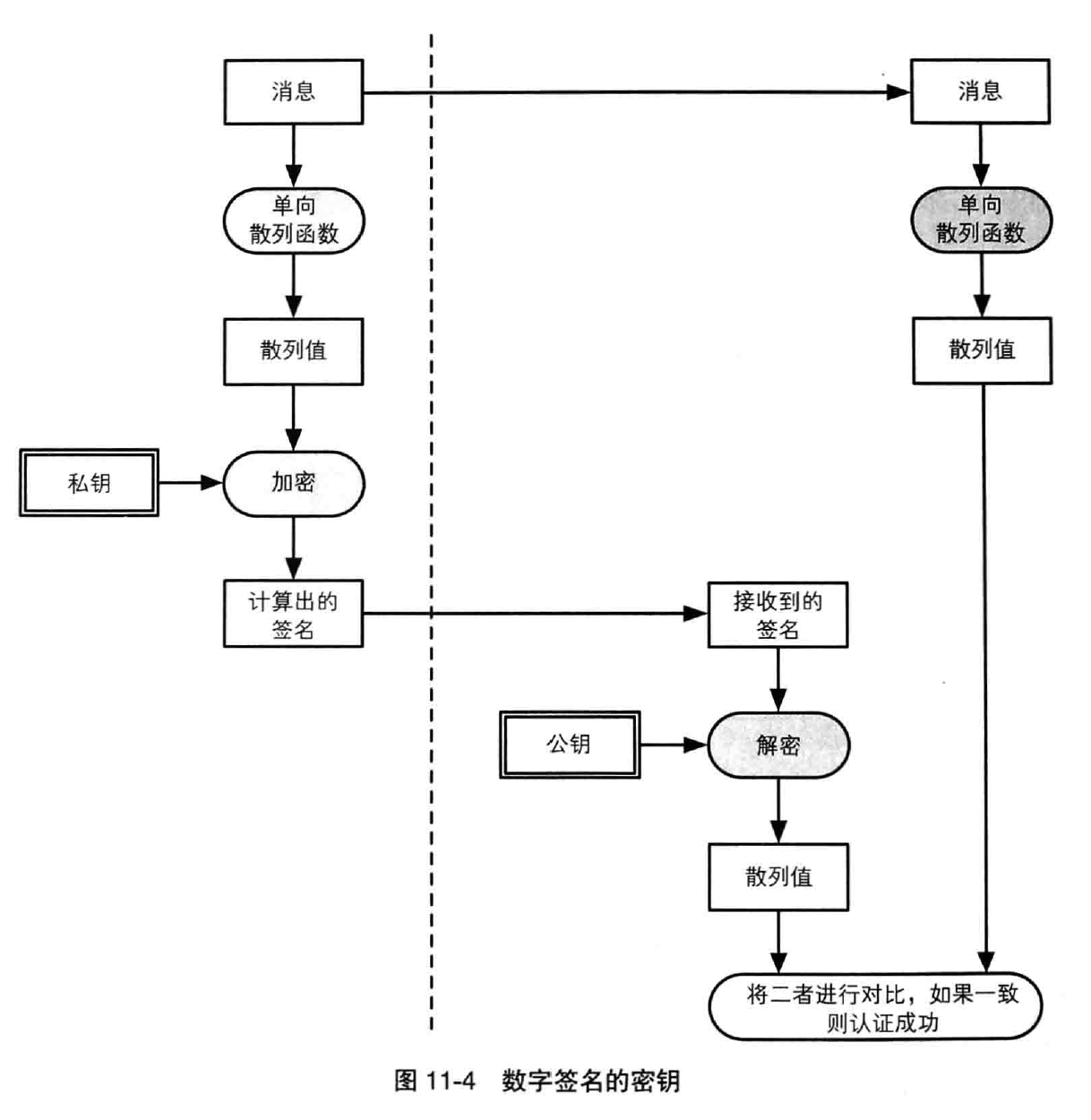
3.4 数字签名

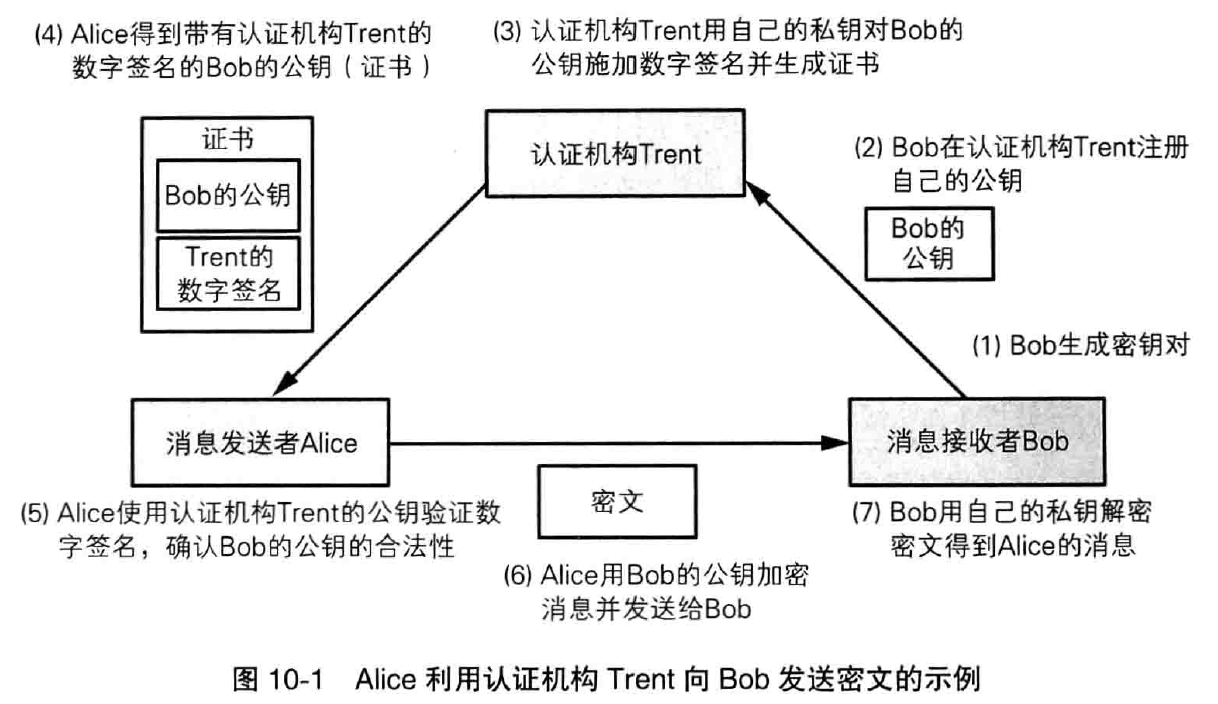
数字签名是现实社会中的签名（sign）和盖章这样的行为在数字世界中的实现。数字签名的处理过程非常耗时，因此一般不会对整个消息内容直接施加数字签名，而是先通过单向散列函数计算出消息的散列值，然后再对这个散列值施加数字签名，将在第九章详解。

3.5 伪随机数生成器

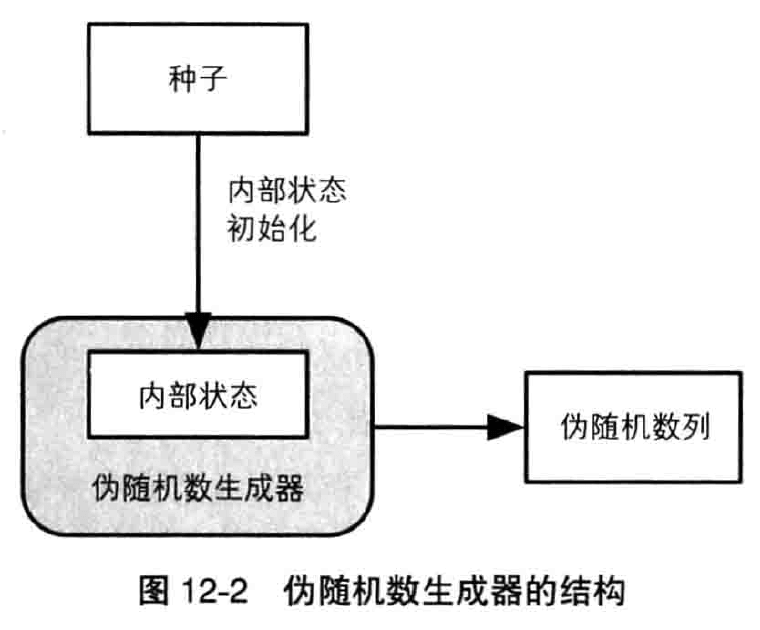
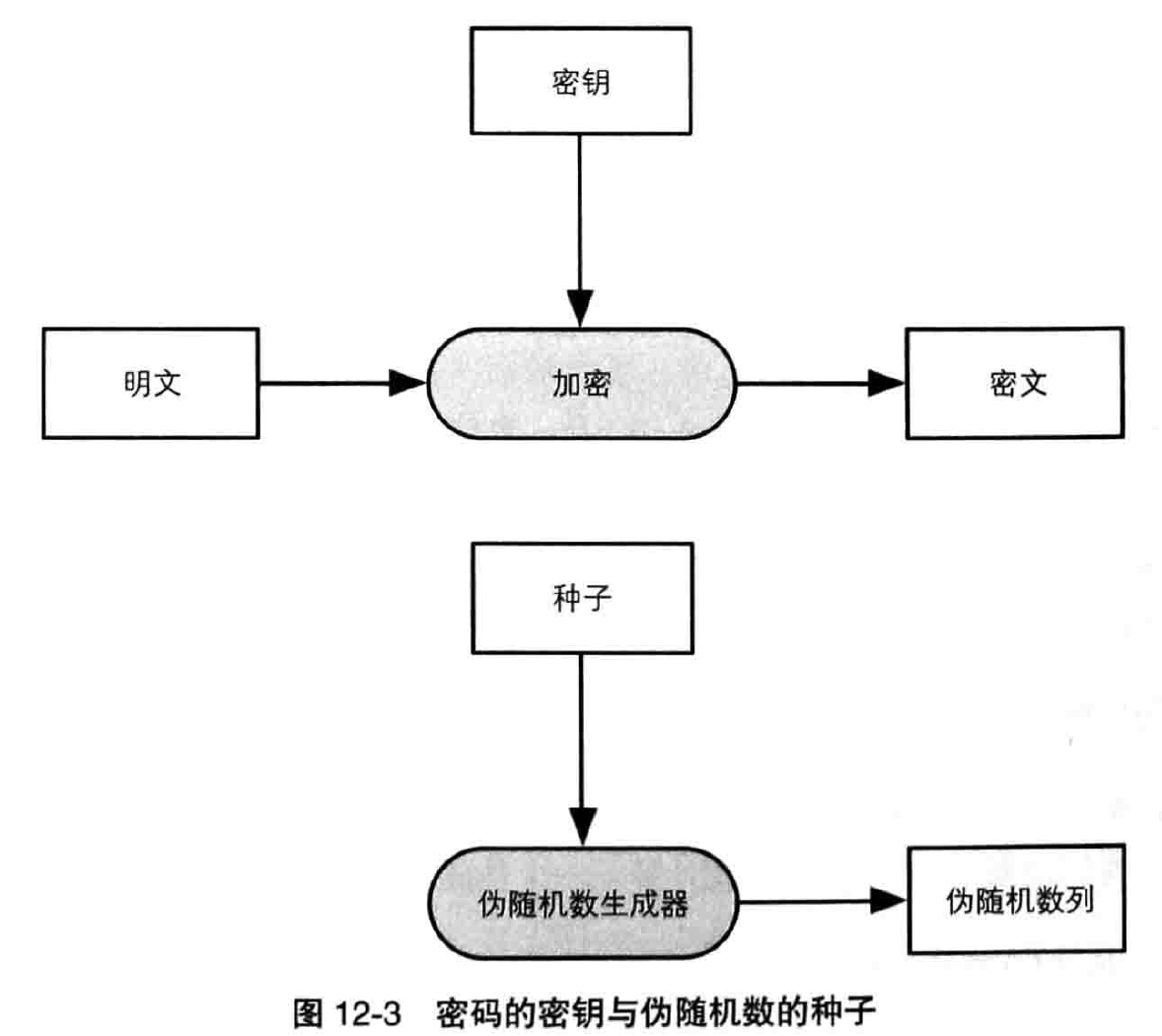
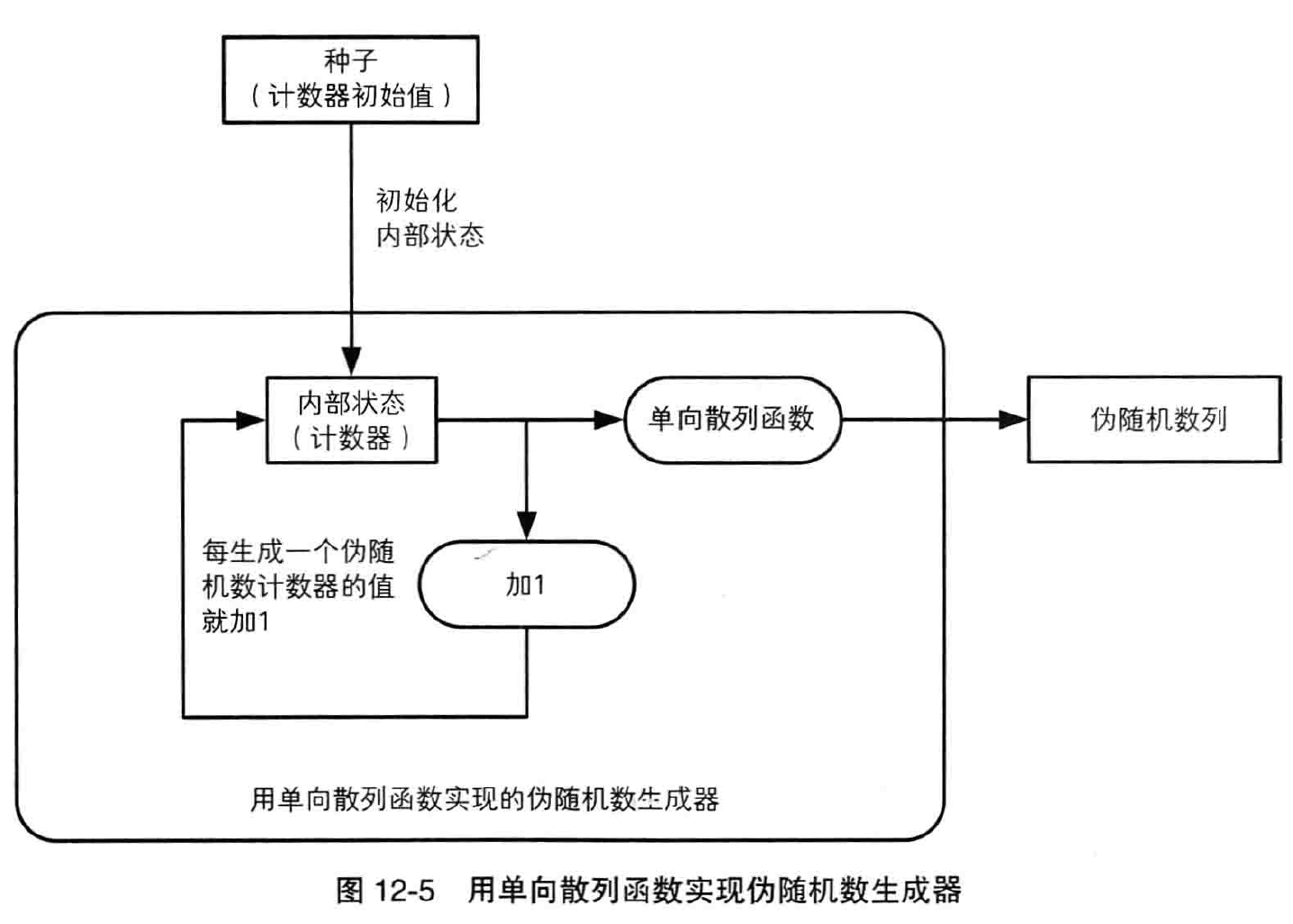
使用单向散列函数可以构造伪随机数生成器。
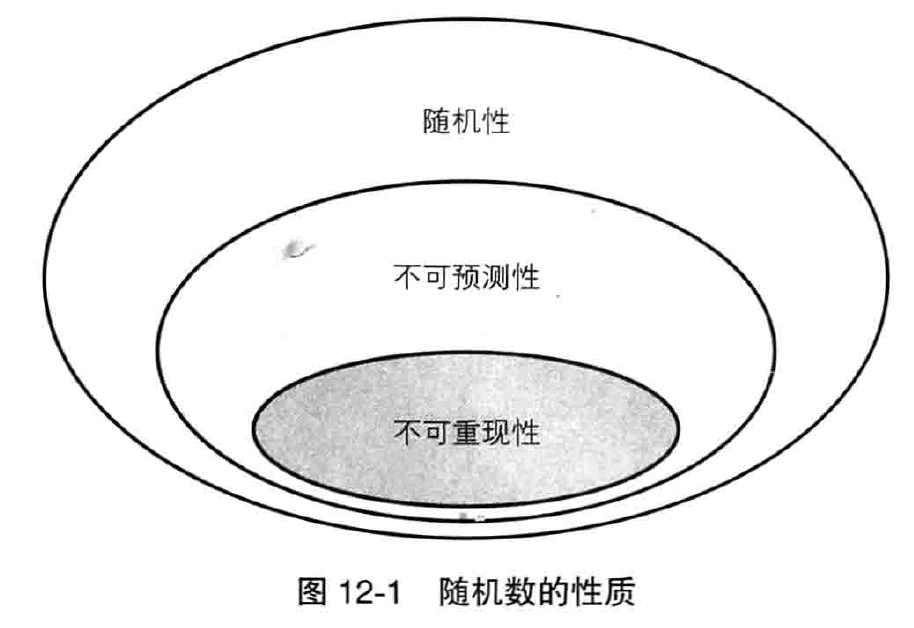
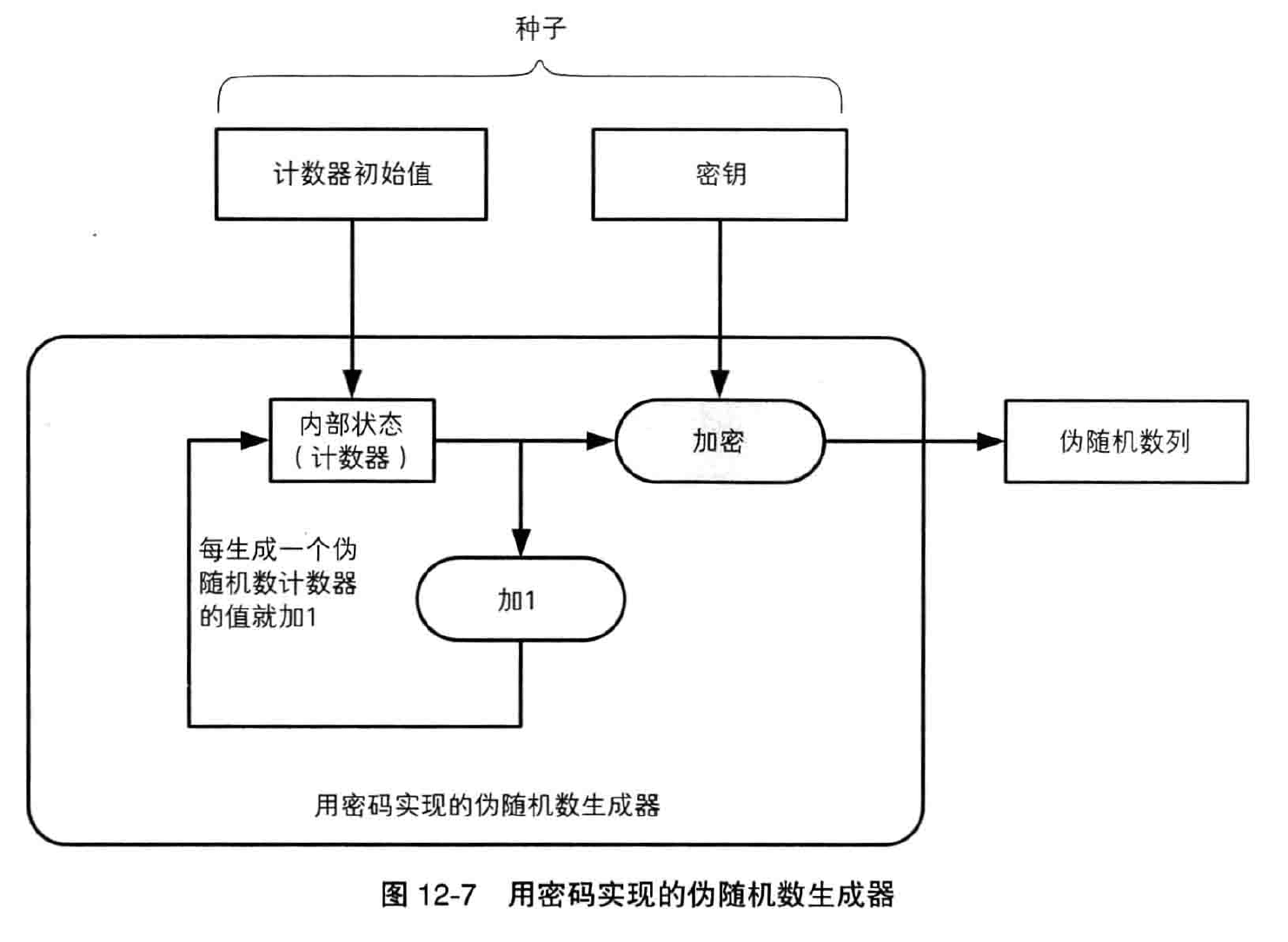
密码技术中所使用的随机数需要具备“事实上不可能根据过去的随机数列预测未来的随机数列”这样的性质。为了保证不可预测性，可以利用单向散列函数的单向性，将在第十二章详解。

3.6 一次性口令

一次性口令（one-time password），经常被用于服务器对客户端的合法性认证，在这种方式中，通过使用单向散列函数可以保证口令只在通信链路上传送一次（one-time），因此即使窃听者窃取了口令，也无法使用。

4 单向散列函数的具体例子

4.1 MD4、MD5

MD4 是由 Rivest 于 1990 年设计的单向散列函数，能够产生 128 比特的散列值，由于寻找到了 MD4 散列碰撞的方法，因此现在它已经不安全了。
MD5 是由 Rivest 于 1991 年设计的单向散列函数，能够产生 128 比特的散列值，由于 MD5 的强抗碰撞性已经被攻破，也就是说，现在已经能够产生具有相同散列值的两条不同的消息，因此它也已经不安全了。
MD 是消息摘要（Message Digest）的缩写。

4.2 SHA-1、SHA-256、SHA-384、SHA-512

SHA-1 是由 NIST（National Institute of Standards and Technology，美国国家标准技术研究所）设计的一种能够产生 160 比特的散列值的单向散列函数。
SHA-256、SHA-384、SHA-512 都是由 NIST 设计的单向散列函数，它们的散列值长度分别为 256 比特、384 比特、512 比特。统称为 SHA-2。
它们的消息长度都存在上限。SHA-1 的强抗碰撞性已于 2005 年被攻破，也就是说，现在已经能够产生具备相同散列值的两条不同的消息。不过，SHA-2 还尚未被攻破。

4.3 RIPEMD-160

RIPEMD-160 是 1996 年设计的一种能够产生 160 比特的散列值的单向散列函数。RIPEMD 的强抗碰撞性已于 2004 年被攻破，但 RIPEMD-160 还尚未被攻破。

4.4 AHS（Advanced Hash Standard）与 SHA-3

在 2005 年 SHA-1 的强抗碰撞性被攻破的背景下， NIST 开始着手制定用于取代 SHA-1 的下一代单向散列函数 SHA-3 。SHA-3 和 AES 一样采用公开竞赛的方式进行标准化。

5 单向散列函数 SHA-1

此章主要讲解其具体算法，有感兴趣者请看原书。

6 对单向散列函数的攻击

6.1 暴力破解（攻击故事 1 ）

Alice 在计算机上写了一份合同。晚上，攻击者 Mallory 入侵了计算机，他想将其中的：

Alice 要支付的金额为 100 万元。

改成：

Alice 要支付的金额为 1 亿元。

不过，不仅要修改合同内容，还要不能改变散列值。
Mallory 可以从文档文件所具有的冗余性入手。所谓文档文件的冗余性，是指在不改变文档意思的前提下能够对文件的内容进行修改的程度。
举个例子，下面的这些句子基本上说的都是一个意思：
Alice 要支付的金额为 1 亿元。
Alice 要支付的金额为壹亿元。
Alice 要支付的金额为 100000000 元。
Alice 应支付 1 亿元。
作为报酬， Alice 需要支付 1 亿元。

除此之外，还有一些通过机器来进行修改的方法。例如，可以在文件的末尾添加 1 个、2 个、3 个甚至更多的空格，或者还可以对文档中的每一个字稍微改变一些颜色，这都不会影响文档的意思。在这里需要注意的是，即便我们对文件所进行的修改是无法被人类察觉的，但只要是对文件进行了修改，单向散列函数就会产生不同的散列值。

于是，Mallory 利用文档的冗余性，通过机器生成了一大推“支付一亿元的合同”。如果在这一大推合同中，能够找到一个合同和 Alice 原本的“ 100 万元合同”恰好产生相同的散列值，那 Mallory 就算是成功了。
在这里，Mallory 所进行的攻击就是暴力攻击。正如对密码可以进行暴力破解一样，对单向散列函数也可以进行暴力破解。这相当于一种试图破解单向散列函数的“弱抗碰撞性”的攻击。在这种情况下，暴力破解需要尝试的次数可以根据散列值得长度计算出来。以 SHA-1 为例，由于它的散列值长度为 160 比特，因此最多只要尝试 2160 次就能够找到目标消息了。（这里不懂为什么是 2160 次）

6.2 生日攻击（攻击故事 2 ）

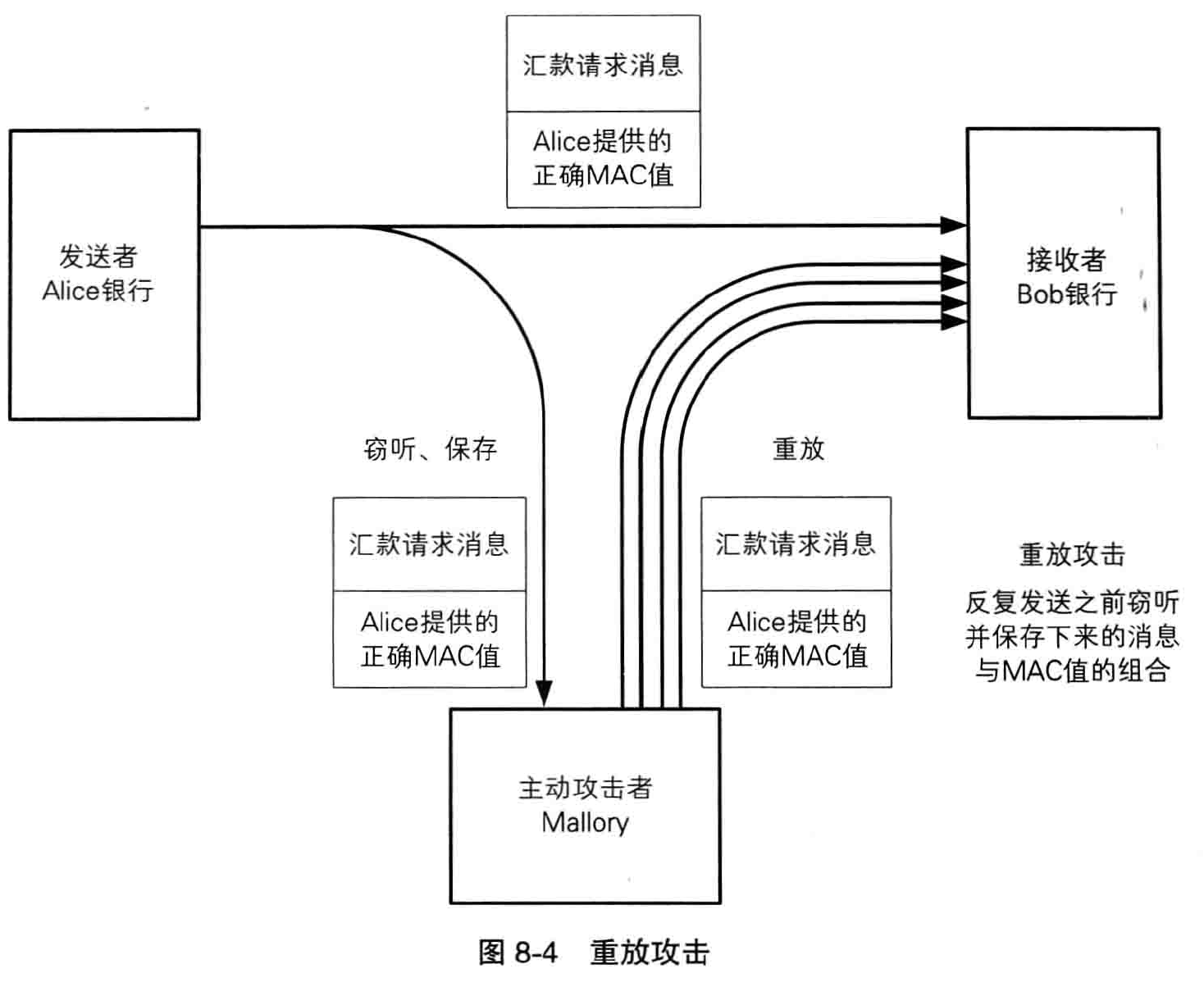
编写合同的人不是 Alice 而是主动攻击者 Mallory 。 Mallory 事先准备两份具备相同散列值的“100 万元合同”和“一亿元合同”，然后将“100 万元合同”交给 Alice 让她计算散列值。随后， Mallory 再像故事 1 中一样， 掉包合同。
这里 Mallory 所进行的攻击不是寻找生成特定散列值的消息，而是要找到散列值相同的两条消息，而散列值可以是任意值。这样的攻击，一般称为生日攻击（birthday attack），这是一种试图破解单向散列函数的“强抗碰撞性”的攻击。
这里存在一个生日驳论的数学思想，有兴趣的请自行谷歌。

7 单向散列函数无法解决的问题

假如，攻击者 Mallory 伪装成 Alice ，向 Bob 同时发送了消息和散列值。Bob 通过单向散列函数检查消息的完整性，但是无法检查出发送者的身份是否被 Mallory 进行了伪装。也就是说，单向散列函数能够辨别出“篡改”，但无法辨别出“伪装”。
因此我们还需要进行认证，用于认证的技术包括消息认证码和数字签名。消息认证码能够向通信对象保证消息没有被篡改，而数字签名不仅能够向通信对象保证消息没有被篡改，还能够向所有第三方作出这样的保证。
认证需要使用秘钥，也就是通过对消息附加 Alice 的秘钥（只有 Alice 才知道的密码信息）来确保消息真的属于 Alice。

8 本章小结

本章学习了用于确认消息完整性的单向散列函数，其能够根据任意长度的消息计算出固定长度的散列值，通过对比散列值就可以判断两条消息是否一致。这种技术对辨别篡改非常有效。
以及学习了代表性的单向散列函数——SHA-1的实现方法以及破解方法——暴力破解和生日攻击。
但是，单向散列函数，虽然可以辨别出篡改，但无法辨别伪装。要解决这个问题，我们需要消息验证码和数字签名。将在下一章介绍消息验证码。

9 小测验

1. MD5 是一种能够将任意长度的数据转换为 128 比特的对称密码算法。
2. 要找出和某条消息具备相同散列值的另一条消息是非常困难的。
3. 要找出具有相同散列值但互不相同的两条消息是非常困难的。
4. SHA-1 的散列值长度为 20字节。
5. 如果消息仅被改写了 1 比特，则散列值也仅发生 1 比特的改变。

1 混合动力汽车

在介绍混合密码系统之前，我们先来说说混合动力汽车。混合动力汽车同时装备了电动机和发动机两种动力系统。
电动机由电池驱动，发动机由汽油驱动。当速度较慢时，汽车由电动机驱动，能够安静地行驶。当速度加快时，动力切换到发动机，以便输出更强的动力。
当踩下刹车时，损失的能量中的一部分能够被回收并用来对电池进行充电。

混合动力汽车将电动机和发动机两种不同的动力融合在一起，从而发挥了两种动力各自的优势。

2 本章概要

本章将学习由对称密码和公钥密码相结合的混合密码系统。

混合密码系统由对称密码来加密明文，用公钥密码来加密对称密码中所使用的密码。通过使用混合密码系统，就能够在通信中将对称密码和公钥密码的优势结合起来。

3 混合密码系统

3.1 对称密码和公钥密码

对称密码存在秘钥配送问题，而公钥密码虽然解决了秘钥配送问题，但是还有两个很大的问题：

1. 公钥密码的处理速度远远低于对称密码
2. 公钥密码难以抵御中间人攻击

本章介绍的混合密码系统就是解决问题 1 。而解决问题 2 则需要对公钥进行认证，将在第十章进行介绍

3.2 混合密码系统

1. 用对称密码加密信息
2. 通过伪随机数生成器生成对称密码的会话秘钥
3. 通过公钥密码加密会话秘钥
4. 从混合密码系统外部赋予公钥密码加密时使用的秘钥

混合密码系统运行了伪随机数生成器、对称密码和公钥密码这三种密码技术。正是通过这三种密码技术的结合，才创造出了一种兼具对称密码和公钥密码优点的密码方式。
即利用了对称密码的解密速度，公钥密码的机密性。

3.3 加密

流程图如下：

1. 明文、秘钥、密文

首先看中间虚线围成的大方框，这里就是混合密码系统的加密部分。
上面标有“消息”的方框就是混合密码系统中的明文，左边标有“接收者的公钥”的方框就是混合密码系统中的秘钥，而下面标有“用公钥密码加密加密的会话秘钥”和
“用对称密码加密的消息”所组成的方框，就是混合密码系统中的密文。

2. 加密消息

中间的大虚线方框分成左右两部分。
右半部分是“加密消息”的部分（对称密码），左半部分是“加密会话秘钥”的部分（公钥密码）。
消息的加密方法和对称密码的一般加密方法相同，当消息很长时，则需要使用第四章介绍的分组密码 的模式。即便是非常长的消息，也可以通过对称密码快速完成加密。
这就是右半部分所进行的处理。

3. 加密会话秘钥

左半部分进行的是会话秘钥的生成和加密操作。
会话秘钥（session key）是指为本次通信而生成的临时秘钥，它一般是通过伪随机数生成器产生的。伪随机数生成器所产生的会话秘钥同时也会被传递给右半部分，
作为对称密码的秘钥使用。
接下来，通过公钥密码对会话秘钥进行加密，公钥密码加密所使用的秘钥是接收者的公钥。

会话秘钥是对称密码的秘钥，同时也是公钥密码的明文。请大家一定要理解会话秘钥的双重性！

4. 组合

如何上面的内容都理解了，剩下的就简单多了。
我们从右半部分可以得到“用对称密码加密的消息”，从左半部分可以得到“用公钥密码加密的会话秘钥”，然后我们将两者组合起来。所谓组合，就是把它们按顺序拼在一起。
组合之后的数据就是混合密码系统整体的密文。

3.4 解密

流程图如下：

1. 分离

只要发送者和接收者事先先约定好密文的结构，将“用公钥密码加密的会话秘钥”和“用对称密码加密的消息”分离的操作就很容易完成。

2. 解密会话秘钥

会话秘钥可以用公钥密码进行解密，为此我们就需要解密秘钥，也就是接收者的私钥。除了持有私钥的人以外，其他人都不能够解密会话秘钥。
解密后的会话秘钥将被用作解密消息的秘钥。

3. 解密消息

消息可以使用对称密码进行解密，解密的秘钥就是刚刚用公钥解密的会话秘钥。
上述流程正好是“混合密码系统的加密”的逆操作。

3.5 混合密码系统的具体例子

混合密码系统解决了公钥密码速度慢的问题，并通过公钥密码解决了对称密码的秘钥配送问题。
著名的密码软件 PGP、 以及网络上的密码通信所使用的 SSL/TLS 都运用了混合密码系统，具体在第十三章探讨。

4 怎样才是高强度的混合密码系统

4.1 伪随机数生成器

混合密码系统中，随机数生成器被用于产生会话秘钥。如果伪随机数生成器的算法很差，生成的会话秘钥就有可能被攻击者推测出来。
会话秘钥中哪怕只有部分比特被推测出来也是很危险的，因为会话秘钥的秘钥空间不大。很容易通过暴力破解来发动攻击。关于针对伪随机数生成器的
攻击方法，将在第十二章详解。

4.2 对称密码

混合密码系统中，对称密码被用于加密消息。当然，我们还需要使用高强度的对称密码算法，并确保秘钥具有足够的长度。此外，我们还需要选择合适的分组密码模式。

4.3 公钥密码

混合密码系统中，公钥密码被用于加密会话秘钥。我们需要使用高强度的公钥密码算法，并确保秘钥具有足够的长度。

4.4 秘钥长度的平衡

对称密码和公钥密码的秘钥长度必须具备同等的强度。
然而，考虑到长期运用的情况，公钥密码的强度应该要高于对称密码，因为对称密码的会话秘钥被破译只会影响本次通信的内容，而公钥密码一旦被破译，从过去到未来的（用相同公钥加密的）所有通信内容就能够被破译了。

5 密码技术的组合

本章介绍的混合密码系统是将对称密码和公钥密码的结合，从而构建出一种同时发挥两者优势的系统。密码技术的组合经常被用于构建一些实用的系统。
例如，第四章中介绍的分组密码模式，就是将只能加密固定长度的数据的 分组密码进行组合，从而使其能够对更长的明文进行加密的方法。通过采用不同的分组密码组合方式，我们就可以构建出各种具有不同特点的分组密码模式。

三重 DES是将 3 个 DES 组合在一起，从而形成一种秘钥比 DES 更长的对称密码。通过加密-解密-加密这样的连接方式，不但可以维持和 DES 的兼容性，同时还能够选择性地使用 DES-DES2 这种秘钥长度较短的密码。

对称密码的内部也存在一些有趣的节后。例如第三章中介绍的 Feistel 网络，不管轮函数的性质如何，它都能够保证密码被解密。
在本书剩下的章节中，还会出现一些由多种技术组合而成的技术，我们来做一个简单的介绍。

数字签名，是由单向散列函数和公钥密码组合而成的。
证书，是由公钥和数字签名组合而成的。
消息认证码，是由单向散列函数和秘钥组合而成的，也可以通过对称密码来生成。
伪随机数生成器，可以使用对称密码、单向散列函数或者公钥密码来构建。
还有一些很神奇的系统，例如电子投票、电子货币、能够在不知道内容的情况下签名的盲签名（zero-knowledge proof）等。

6 本章小结

本章中我们学习了将对称密码和公钥密码的优势相结合而成的混合密码系统。
到此为止，我们已经了解了密码这一保证机密性的技术，然而，密码技术所保护的不仅仅是机密性。
从下一章开始，我们将学习确认消息完整性、进行认证以及防止否认的技术。

7 小测验

1. 混合密码系统是用对称密码对消息进行加密的。
2. 混合密码系统是用公钥密码的私钥对对称密码的秘钥进行加密的。
3. 由于会话秘钥已经通过公钥密码进行了加密，因此会话秘钥的长度较短也没有问题。
4. 混合密码系统的解密过程是按照“公钥密码解密”->“对称密码解密”的顺序来进行处理的。